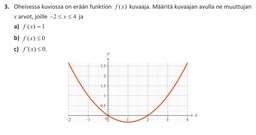
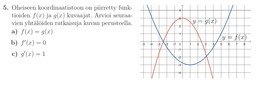
10. Derivointi (bonus)
Miten lasket derivaatan arvoja?
Merkitseminen:
Derivaatan arvoja voidaan laskea funktioille tai esimerkiksi polynomeille. Funktion [[$ f $]] derivaattaa merkitään [[$ f' $]]. Vastaavasti lausekkeiden derivaattoja merkitään yleisesti kirjaimella [[$D$]], esimerkiksi lausekkeen [[$x^2$]] derivaatta on [[$D(x^2)=2x$]].
Vakion derivaatta:
Vakion derivaatta on aina 0.
[[$ D(1) = 0$]]
[[$ D(5) = 0$]]
[[$ D(0) = 0$]]
[[$ D(2) = 0$]]
Muuttujan sisältävän termin derivaatta:
Muuttujan sisältävän termin derivaatta saadaan kertomalla termi sen asteluvulla, ja pienentämällä sen astelukua yhdellä. Muuttujan eksponentti siis siirtyy siis termin eteen kertoimeksi (mikäli edessä on jo kerroin, kerrotaan se tällä asteluvulla), ja muuttujan eksponenttia pienennetään yhdellä.
[[$ D(x^2) = 2x $]]
[[$ D(x^3) = 3x^2 $]]
[[$ D(x^{10}) = 10x^9$]]
[[$ D(x^{100})=100x^{99}$]]
[[$ D(2x^2) = 2\cdot 2x^{2-1} = 4x $]]
[[$ D(3x^5) = 5\cdot 3x^{5-1} = 15x^4$]]
[[$ D(6x^{10}) =10\cdot 6x^{10-1} = 60x^9$]]
Ensimmäisen asteen termin derivoiminen:
Jos derivoitavan termin asteluku on 1, derivointi tapahtuu vastaavasti kuin yllä:
[[$ D(x) = 1\cdot x^{1-1} = 1\cdot x^0 = 1\cdot 1 = 1 $]]
[[$ D(5x) = 5\cdot x^{1-1} = 5\cdot x^0 = 5\cdot 1 = 5 $]]
Ensimmäisen asteen termin derivaatta on näin siis aina sama kuin tämän ensimmäisen asteen termin kerroin, eli
[[$ D(x) = 1 $]]
[[$ D(2x) = 2$]]
[[$ D(10x) = 10$]]
[[$ D(20x) = 20$]]
Yleisesti siis:
[[$ D(x^n) = nx^{n-1}$]]
Polynomin derivoiminen:
Jos derivoitavana on polynomi, derivointi tehdään jokaiselle termille erikseen.
[[$ D(2x^2+2x) = D(2x^2) + D(2x) = 4x + 2 $]]
Funktion derivoiminen:
Funktion derivoiminen tapahtuu vastaavasti kuin edellä, merkintänä käytetään vaan funktiomerkintää. Jos siis pyydetään derivoimaan [[$ f(x) = 3x^2 $]], niin vastaus merkitään [[$f'(x) = 6x$]].
Derivaatan arvoja voidaan laskea funktioille tai esimerkiksi polynomeille. Funktion [[$ f $]] derivaattaa merkitään [[$ f' $]]. Vastaavasti lausekkeiden derivaattoja merkitään yleisesti kirjaimella [[$D$]], esimerkiksi lausekkeen [[$x^2$]] derivaatta on [[$D(x^2)=2x$]].
Vakion derivaatta:
Vakion derivaatta on aina 0.
[[$ D(1) = 0$]]
[[$ D(5) = 0$]]
[[$ D(0) = 0$]]
[[$ D(2) = 0$]]
Muuttujan sisältävän termin derivaatta:
Muuttujan sisältävän termin derivaatta saadaan kertomalla termi sen asteluvulla, ja pienentämällä sen astelukua yhdellä. Muuttujan eksponentti siis siirtyy siis termin eteen kertoimeksi (mikäli edessä on jo kerroin, kerrotaan se tällä asteluvulla), ja muuttujan eksponenttia pienennetään yhdellä.
[[$ D(x^2) = 2x $]]
[[$ D(x^3) = 3x^2 $]]
[[$ D(x^{10}) = 10x^9$]]
[[$ D(x^{100})=100x^{99}$]]
[[$ D(2x^2) = 2\cdot 2x^{2-1} = 4x $]]
[[$ D(3x^5) = 5\cdot 3x^{5-1} = 15x^4$]]
[[$ D(6x^{10}) =10\cdot 6x^{10-1} = 60x^9$]]
Ensimmäisen asteen termin derivoiminen:
Jos derivoitavan termin asteluku on 1, derivointi tapahtuu vastaavasti kuin yllä:
[[$ D(x) = 1\cdot x^{1-1} = 1\cdot x^0 = 1\cdot 1 = 1 $]]
[[$ D(5x) = 5\cdot x^{1-1} = 5\cdot x^0 = 5\cdot 1 = 5 $]]
Ensimmäisen asteen termin derivaatta on näin siis aina sama kuin tämän ensimmäisen asteen termin kerroin, eli
[[$ D(x) = 1 $]]
[[$ D(2x) = 2$]]
[[$ D(10x) = 10$]]
[[$ D(20x) = 20$]]
Yleisesti siis:
[[$ D(x^n) = nx^{n-1}$]]
Polynomin derivoiminen:
Jos derivoitavana on polynomi, derivointi tehdään jokaiselle termille erikseen.
[[$ D(2x^2+2x) = D(2x^2) + D(2x) = 4x + 2 $]]
Funktion derivoiminen:
Funktion derivoiminen tapahtuu vastaavasti kuin edellä, merkintänä käytetään vaan funktiomerkintää. Jos siis pyydetään derivoimaan [[$ f(x) = 3x^2 $]], niin vastaus merkitään [[$f'(x) = 6x$]].
Derivoi
Mitä derivaatta tarkoittaa ja mihin sitä käytetään?
Derivaatta kertoo funktion kasvunopeuden. Esimerkiksi funktion [[$ f(x) = 2x^2-3x$]] derivaatta on [[$ f'(x) = 4x-3$]], joten sen kasvunopeus
pisteessä 2 on [[$ f(2) = 4\cdot 2-3 = 8-3 = 5$]] . Oikeanpuoleisessa kuvassa ollaan zoomattu funktioon kohdan [[$x=2$]] lähelle, ja funktio tosiaankin näyttää kasvavan tässä kohdassa n. 5 ruutua yhden vaakaruudun aikana.


Lukiomatikassa ja YO-kirjoituksissa derivaatan suosituin käyttätarkoitus on funktion suurimpien ja pienimpien arvojen etsiminen. Nämä kohdat ovat yleensä funktion derivaatan nollakohdissa. Esimerkiksi ylläolevan funktion derivaatta oli [[$ f'(x) = 4x-3$]], josta voidaan laskea derivaatan nollakohta: jos [[$f'(x) = 4x-3 = 0$]], on oltava [[$x=\frac{3}{4}$]]. Ylläolevasta kuvasta näkyy, että funktio saa tässä pienimmän arvonsa, joka on
[[$f(\cfrac{3}{4}) = 2(\cfrac{3}{4})^2-3\cdot \cfrac{3}{4} = -\cfrac{9}{8} $]]
Derivaatan nollakohdan lisäksi funktion suurin arvo voi olla sen määrittelyvälin päätepisteissä tai epäderivoituvuus/-jatkuvuuskohdissa. Tästä enemmän oppikirjoissa.
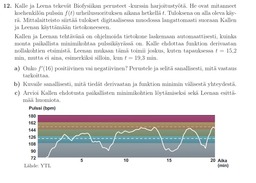
Esimerkki.
Kahvilan katuterassin aitaamiseen on käytettävissä 15 metriä köyttä. Terassista tehdään suorakulmio, ja yksi sitä rajaava sivu on ravintolan seinä. Mitkä terassin sivujen mitat on oltava, että sen pinta-ala olisi mahdollisimman suuri? Mikä pinta-ala tällöin on?
Ratkaisu.
Piiretään ensin kuva:

Vasemmalla mustalla on kahvilan seinä ja punaisella on terassia rajaava köysi. Jos merkataan kahta samanpituista sivua [[$x$]]:llä, kolmanteen sivuun jää köyttä [[$15-2x$]] metriä. Tällöin terassin pinta-ala on [[$A(x) = x\cdot (15-2x) = 15x-2x^2 $]].
Derivoidaan pinta-alan funktio: [[$ A'(x) = 15-4x$]]. Lasketaan derivaatan nollakohta: [[$15-4x=0$]], jos [[$4x=15$]], eli jos [[$x=3.75$]].
Tällöin kolmannen sivun pituus on [[$15-2\cdot 3.75 = 7.5$]] metriä, ja terassin mittojen pitäisi siis olla 3.75m x 7.5 m. Suurin mahdollinen pinta-ala terassille on siis [[$3.75\cdot 7.5 = 28.125 m^2$]]
pisteessä 2 on [[$ f(2) = 4\cdot 2-3 = 8-3 = 5$]] . Oikeanpuoleisessa kuvassa ollaan zoomattu funktioon kohdan [[$x=2$]] lähelle, ja funktio tosiaankin näyttää kasvavan tässä kohdassa n. 5 ruutua yhden vaakaruudun aikana.


Lukiomatikassa ja YO-kirjoituksissa derivaatan suosituin käyttätarkoitus on funktion suurimpien ja pienimpien arvojen etsiminen. Nämä kohdat ovat yleensä funktion derivaatan nollakohdissa. Esimerkiksi ylläolevan funktion derivaatta oli [[$ f'(x) = 4x-3$]], josta voidaan laskea derivaatan nollakohta: jos [[$f'(x) = 4x-3 = 0$]], on oltava [[$x=\frac{3}{4}$]]. Ylläolevasta kuvasta näkyy, että funktio saa tässä pienimmän arvonsa, joka on
[[$f(\cfrac{3}{4}) = 2(\cfrac{3}{4})^2-3\cdot \cfrac{3}{4} = -\cfrac{9}{8} $]]
Derivaatan nollakohdan lisäksi funktion suurin arvo voi olla sen määrittelyvälin päätepisteissä tai epäderivoituvuus/-jatkuvuuskohdissa. Tästä enemmän oppikirjoissa.
Esimerkki.
Kahvilan katuterassin aitaamiseen on käytettävissä 15 metriä köyttä. Terassista tehdään suorakulmio, ja yksi sitä rajaava sivu on ravintolan seinä. Mitkä terassin sivujen mitat on oltava, että sen pinta-ala olisi mahdollisimman suuri? Mikä pinta-ala tällöin on?
Ratkaisu.
Piiretään ensin kuva:

Vasemmalla mustalla on kahvilan seinä ja punaisella on terassia rajaava köysi. Jos merkataan kahta samanpituista sivua [[$x$]]:llä, kolmanteen sivuun jää köyttä [[$15-2x$]] metriä. Tällöin terassin pinta-ala on [[$A(x) = x\cdot (15-2x) = 15x-2x^2 $]].
Derivoidaan pinta-alan funktio: [[$ A'(x) = 15-4x$]]. Lasketaan derivaatan nollakohta: [[$15-4x=0$]], jos [[$4x=15$]], eli jos [[$x=3.75$]].
Tällöin kolmannen sivun pituus on [[$15-2\cdot 3.75 = 7.5$]] metriä, ja terassin mittojen pitäisi siis olla 3.75m x 7.5 m. Suurin mahdollinen pinta-ala terassille on siis [[$3.75\cdot 7.5 = 28.125 m^2$]]
YO-tehtäviä
Derivointi
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.