8.1 Laskeminen funktioilla

Processing ohjelman matemaattiset funktiot

Processing-ohjelman mukana tulee valmiita funktioita laskemiseen. Esitetään niistä tässä yleisimmät.

Processing-ohjelman yleisimmät valmiit funktiot
FUNKTIOMERKITYSESIMERKKI
sq(luku) Luvun neliö sq(3)= 9
sqrt(luku) Luvun neliöjuuri sqrt(25) = 5
nfc(a,n) Pyöristää luvun a n:n desimaalin tarkkuudella. nfc(12.451,1) = 12.5
pow(a,n) Kantaluvun a eksponentti n pow(2,3) = 8
max(a,b) Luvuista suurempi max(3,6) = 6
min(a,b) Luvuista pienempi min(3,6) = 3
abs(luku) Luvun itseisarvo abs(-4) = 4
ceil(luku) Lukua suurempi kokonaisluku ceil(6.7) = 6
floor(luku) Lukua pienempi kokonaisluku ceil(6.7) = 7
norm(luku,min,max) Muuttaa luvun 0:n ja 1:n välissä olevaksi desimaaliluvuksi. norm(20,0,50)=0.4
round(luku) Pyöristää luvun round(5.6) = 6
PI Ilmoittaa piin arvon 3.142
radians(kulma) Muuttaa asteet radiaaneiksi radians(180)=3.142
degrees(kulma) Muuttaa radiaanit asteiksi degrees(PI/2)=90.000
sin(kulma) Kulman sini sin(radians(30)) =0.5
cos(kulma) Kulma kosini cos(radians(30))=0.87
tan(kulma) Kulman tangentti tan(radians(30))=0.58
asin(kulma) Sinin käänteisfunktio degrees(asin(0.5)))=30
acos(kulma) Kosinin käänteisfunktio degrees(acos(0.5))=60
atan(kulma) Tangentin käänteisfunktio degrees(atan(1))=45
atan2(x,y) Origosta lähtevän viivan ja pystyakselin välinen kulma degrees(atan2(3,4))=37
dist(x1,y1,x2,y2) Kahden pisteen välinen etäisyys dist(0,0,3,4)=5
mag(x,y) Pisteen etäisyys origosta mag(3,4)=5

Katsotaan seuraavaksi funktioiden käyttöä esimerkkien avulla. Tässä kappaleessa ei ole tehtäviä, vaan näitä esimerkkejä on tarkoitus käydä ja soveltaa samalla, kun asiaa käydään läpi matematiikan kirjassa.

Polynomin arvon laskeminen

Haluamme laskea polynomin f(x) = x2 –3x + 5 arvon, kun x = –5. Ohjelma, joka laskee sen, on seuraava.

// Ohjelman tehnyt e-Oppi Oy

// 30.8.2017

void setup () {

     size(400,200); // Ikkunan koko

     background(255); // Taustaväri valkoinen

     textSize(24); // Tekstin koko

     fill(0); // Tekstin väri musta

}



void draw () {

     float x = -5;  // Muuttujan arvo

     float y = sq(x)-3*x+5; // Polynomin arvo

     text("f(x) = x\u00B2-3x+5",10,50); // Tulostetaan lauseke

     text("f("+x+") = "+y,10,100); // Tulostetaan muuttujat

}

Ohjelma tulostaa seuraavaa.

Hypotenuusan laskeminen suorakulmaisesta kolmiosta

Haluamme laskea suorakulmaisesta kolmiosta hypotenuusan arvon, kun kateetit ovat 7 ja 12. Ohjelma, joka laskee hypotenuusan arvon, on seuraava.

// Ohjelman tehnyt e-Oppi Oy

// 30.8.2017

void setup () {

     size(500,250); // Ikkunan koko

     background(255); // Taustaväri valkoinen

     textSize(24); // Tekstin koko

     fill(0); // Tekstin väri musta

}



void draw () {

     float a = 7; // Kateetit

     float b= 12;

     float c = sqrt(sq(a)+sq(b));  // Hypotenuusan arvo

     text("Suorakulmaisen kolmion kateetit ovat: ",10,50);

     text("a = "+a,10,100);

     text("b = "+b,10,150);

     text("Hypotenuusa c = "+nfc(c,1),10,200); // Pyöristys 1-desimaalin tarkkuudella

}


Ohjelma tulostaa seuraavaa.



Muuttujan c-arvo voidaan myös laskea seuraavasti:

  float c = mag(a,b);  // Hypotenuusan arvo

Periaatteessa mag()-funktio laskee pisteen etäisyyden origosta. Mutta soveltuu myös hypotenuusan laskemiseen.

Eksponentin laskeminen

Lasketaan potenssien arvoja.

// Ohjelman tehnyt e-Oppi Oy

// 30.8.2017

void setup () {

     size(500,250); // Ikkunan koko

     background(255); // Taustaväri valkoinen

     textSize(24); // Tekstin koko

     fill(0); // Tekstin väri musta

}

void draw () {

     text("2\u2075 = "+pow(2,5),10,50);

     text("5\u00B2 = "+pow(5,2),10,100);

     text("2\u00B3\u00B72\u2074 = 2\u2077 = "+pow(2,7),10,150);

     text("(2\u00B2)\u00B3 ="+pow(pow(2,2),3),10,200);

}

Ohjelma tulostaa seuraavaa.

Suurin ja pienin

Tutkitaan, kumpi muuttujista on suurempi ja kumpi pienempi.

// Ohjelman tehnyt e-Oppi Oy

// 30.8.2017

void setup () {

     size(500,250); // Ikkunan koko

     background(255); // Taustaväri valkoinen

     textSize(24); // Tekstin koko

     fill(0); // Tekstin väri musta

}

void draw () {

     int a = 5;

     int b = 8;

     text("Suurempi luvuista "+a+" ja "+b+" on "+max(a,b),10,100);

     text("Pienempi luvuista "+a+" ja "+b+" on "+min(a,b),10,150);

}

Jolloin ohjelma tulostaa seuraavaa.

Luvun pyöristäminen

Tutkitaan, kuinka lukua voidaan pyöristää.

// Ohjelman tehnyt e-Oppi Oy

// 30.8.2017

void setup () {

     size(500,300); // Ikkunan koko

     background(255); // Taustaväri valkoinen

     textSize(24); // Tekstin koko

     fill(0); // Tekstin väri musta

}



void draw () {

     text(abs(-4.835),10,30); // Itseisarvo

     text(round(-4.835),10,60); // Pyöristys

     text(int(-4.835),10,90); // Kokonaisosa

     text(ceil(-4.835),10,120); // Suurempi kokonaisluku

     text(floor(-4.835),10,150); // Pienempi kokonaisluku

     text(ceil(4.835),10,180); // Suurempi kokonaisluku

     text(floor(4.835),10,210); // Pienempi kokonaisluku

     text(nfc(-4.835,1),10,240); // 1-desimaali

     text(nfc(-4.835,2),10,270); // 2-desimaalia

}

Ohjelma tulostaa seuraavaa.

Kuinka monta prosenttia?

Lasketaan, kuinka monta prosenttia luku a on luvusta b.

// Ohjelman tehnyt e-Oppi Oy

// 30.8.2017

void setup () {

     size(500,300); // Ikkunan koko

     background(255); // Taustaväri valkoinen

     textSize(24); // Tekstin koko

     fill(0); // Tekstin väri musta

}



void draw () {

     float a = 4;

     float b = 14;

     text("Kuinka monta prosenttia "+a+" on "+b+":sta?",10,50);

     text(norm(a,0,b)+" = "+nfc(norm(a,0,b)*100,1)+" %",10,100); 

}

Ohjelma tulostaa seuraavaa. Voit kokeilla muuttaa a:n ja b:n arvoja.

Ympyrän pinta-ala ja piiri

Laskemme ympyrän pinta-alan ja piirin.

// Ohjelman tehnyt e-Oppi Oy

// 30.8.2017

void setup () {

     size(500,200); // Ikkunan koko

     background(255); // Taustaväri valkoinen

     textSize(24); // Tekstin koko

     fill(0); // Tekstin väri musta

}



void draw () {

     float r = 4;

     float A = PI*sq(r);

     float p = 2*PI*r;

     text("Ympyrän säde on "+r+" cm",10,50);

     text("Pinta-ala A = "+nfc(A,1)+" cm\u00B2",10,100);

     text("Piiri p = "+nfc(p,1)+" cm",10,150);

}

Ohjelma tulostaa seuraavaa.

Kulman laskeminen



Haluamme laskea kuvan mukaisen suorakulmaisen kolmion kulmat.

// Ohjelman tehnyt e-Oppi Oy

// 30.8.2017

void setup () {

     size(500,200); // Ikkunan koko

     background(255); // Taustaväri valkoinen

     textSize(24); // Tekstin koko

     fill(0); // Tekstin väri musta

}



void draw () {

     float a = 3.0;

     float b = 4.0;

     float c = 5.0;

     text("\u03B1 ="+nfc(degrees(asin(a/c)),1)+"\u00B0",10,50);

     text("\u03B1 ="+nfc(degrees(acos(b/c)),1)+"\u00B0",10,100);

     text("\u03B2 ="+nfc(degrees(atan(b/a)),1)+"\u00B0",10,150);

}
Ohjelma laskee kulmat ja tulostaa seuraavaa.

Sivun pituuden laskeminen kulman avulla



Haluamme laskea kuvan mukaisesta suorakulmaisesta kolmiosta a:n ja b:n pituudet.

// Ohjelman tehnyt e-Oppi Oy

// 30.8.2017

void setup () {

     size(500,250); // Ikkunan koko

     background(255); // Taustaväri valkoinen

     textSize(24); // Tekstin koko

     fill(0); // Tekstin väri musta

}



void draw () {

     float alfa = 35;

     float beeta = 55;

     float c = 120;

     text("a = "+nfc(c*sin(radians(alfa)),1)+" m",10,50);

     text("b = "+nfc(c*cos(radians(alfa)),1)+" m",10,100);

     text("b = "+nfc(c*sin(radians(beeta)),1)+" m",10,150);

     text("a = "+nfc(c*cos(radians(beeta)),1)+" m",10,200);

}

Tulostuu seuraavaa.

Pisteen etäisyys origosta ja viivan ja pystyakselin välinen kulma

Komennolla dist(x1,y1,x2,y2) voimme selvittää kahden pisteen välisen etäisyyden toisistaan ja komennolla atan2(x,y) voimme laskea origosta lähtevän viivan kierokulman origon ympäri. Oheinen esimerkki havainnollistaa asiaa.

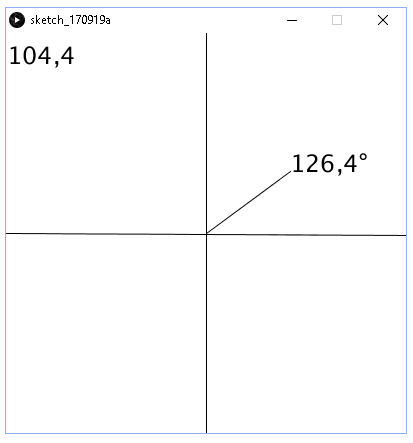
void setup () {

     size(400,400); // Ikkunan koko

     textSize(24); // Tekstin koko

     fill(0); // Tekstin väri musta

}



void draw () {

     background(255); // Taustaväri valkoinen

     translate(200,200); // Origo ikkunan keskelle

     line(-200,0,200,2);  // Vaaka-akseli

     line(0,200,0,-200);  // Pystyakseli

     float x = mouseX-200;  // Lue hiiren koordinaatit

     float y = mouseY-200;  // Lue hiiren koordinaatit

     line(0,0,x,y); // Piirrä viiva origosta

     float kulma=atan2(x,y);  // Laske kulma radiaaneina

     float pituus=dist(0,0,x,y);  // Viivan pituus

     text(nfc(degrees(kulma),1)+"\u00B0",x,y);  // Tulosta kulma asteina

     text(nfc(pituus,1),-200,-170); //Tulosta viivan pituus

}

Kun ajat ohjelman, niin liikuta hiirtä. Ohjelman tulostus on esimerkiksi seuraavanlainen.

Seuraaja

Tehdään ohjelma, jossa ympyrä liikkuu hiiren liikkeiden mukaan. Nuoli on seuraaja, joka menee aina kohti ympyrää. Ohjelman koodi on seuraava.

// Ohjelman tehnyt e-Oppi Oy

// 30.8.2017

int a = 200;  // Nuolen alkukoordinaatti

int b = 200; // Nuolen alkukoordinaatti

void setup () {

     size(400,400); // Ikkunan koko

}

void draw () {

     background(255); // Taustaväri valkoinen 

     float x = mouseX;  // Hiiren vaaka koordinaatti

     float y = mouseY;  // Hiiren pysty koordinaatti

     float kulma = degrees(atan2(x-a,y-b)); // Ympyrän ja hiiren välinen kulma

     pushMatrix();  // Nuolen pyöritys alkaa, muistiin

     translate(a,b);  // Origo nuolen paikkaan

     rotate(radians(90-kulma)); // Käännä nuoli kohti hiirtä

     fill(255,0,0);  // Punainen väri

     noStroke();  // Ei reunaviivaa

     rect(-20,-10,30,20);  // Suorakulmio

     triangle(20,0,0,20,0,-20);  // Kolmio

     popMatrix();  // Nuolen pyöritys loppuu, palauta muistista

     if (a < x) { // Liiku kohti hiirtä

         a++;

     }

     if (a > x) {

         a--;

     }

     if (b < y) {

         b++;

     }

     if (b > y) {

         b--;

     }

     fill(0);  // Musta väri

     ellipse(x,y,20,20);  // Ympyrä eli hiiren kursori

     if((x==a) && (y==b)) { // Jos nuolen koordinaatit = hiiren koordinaatit

         noLoop();  // Lopeta toisto

         textSize(100);  // Tekstin koko 100

         fill(0,0,255);  // Sininen väri

         text("Game",50,150);  // Peli

         text("Over",50,250);  // Loppui

     }

}

Ohjelman idea on se, että laskureilla a ja b liikutaan aina kohti hiirtä. Kun haluamme pyörittää nuolta, niin silloin vain pyörityksen ajaksi siirrämme origon nuolen paikalle. Oikea kulma pyöritykselle voidaan laskea tan2()-funktiolla. Kun nuoli on pyöritetty oikeaan asentoon, niin sen jälkeen palautamme koordinaatiston takaisin popMatrix()-komennolla. Ohjelman suoritus näyttää tältä.