Example 1

Determine the intersection of the line [[$ y = 2x + 2 $]] and the [[$ x $]] axis graphically.



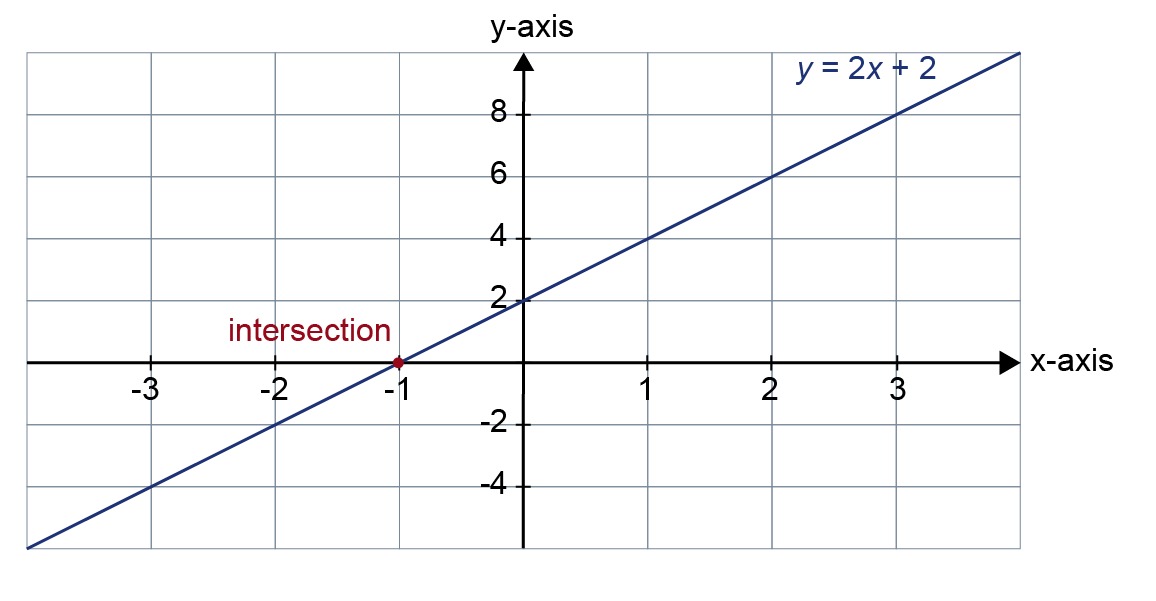
The graph shows that the intersection of the line and the [[$ x $]] axis is [[$ x = -1 $]].

Computationally, the point of intersection is found by solving the equation [[$ 2x + 2 = 0 $]]. Let's take a closer look at how the equation [[$ 2x + 2 = 0 $]] is formed.

[[$$ {\color {red} {\text {The equation of the given line is}}} \;\;\;\;\;\;\;\; {\color {blue} {\text {The equation of the x-axis is}}} $$]]​
[[$$ \color {red} {y = 2x + x} \;\;\;\;\;\;\;\; \color {blue} {y = 0} \\ \\ $$]]​
[[$$ {\color {green} {\text {Both of the equations contain y, so a pair of equations can be combined.}}} $$]]​
[[$$ {\color {red} {2x + 2 =} \color {green} { y } \color {blue} {= 0}} \ \\ $$]]​
It is a combination of two equations, i.e. a pair of equations, usually presented in the form

[[$$ \begin{equation} \begin{cases} y = 2x + 2 \\ y = 0\\ \end{cases} \end{equation} $$]]​

Thus, finding the intersection of two lines means the same thing as solving a pair of equations formed by those equations. The solution of the pair of equations is the points that give the same result, regardless of whether they are placed in either of the two equations.

Determining the coordinates of an intersection graphically always gives an approximate solution to a pair of equations. Exact values for the variables can be obtained only by calculating the pair of equations.

Not all pairs of equations have a solution, whereas some may have an infinite number of them.

Example 2

Solve the following pair of equations:

[[$ \begin{equation} \begin{cases} x - 2y = 1 \\ x + 2y = 5 \\ \end{cases} \end{equation} $]]

First, let's convert the equations to a general form.

[[$ \begin{align*}x - 2y &= 1 \\ -2y &= -x + 1 \\ y &= \displaystyle\frac {1} {2} x - \displaystyle\frac {1} {2} \end{align*} \: \: \: \: \: $]]​
and
[[$ \: \: \: \: \: \begin{align*}x + 2y &= 5 \\ 2y &= -x + 5 \\ y &= -\displaystyle\frac {1} {2} x + \displaystyle\frac {5} {2} \end{align*} $]]​

Next, draw the lines in the same coordinate system and determine their point of intersection.

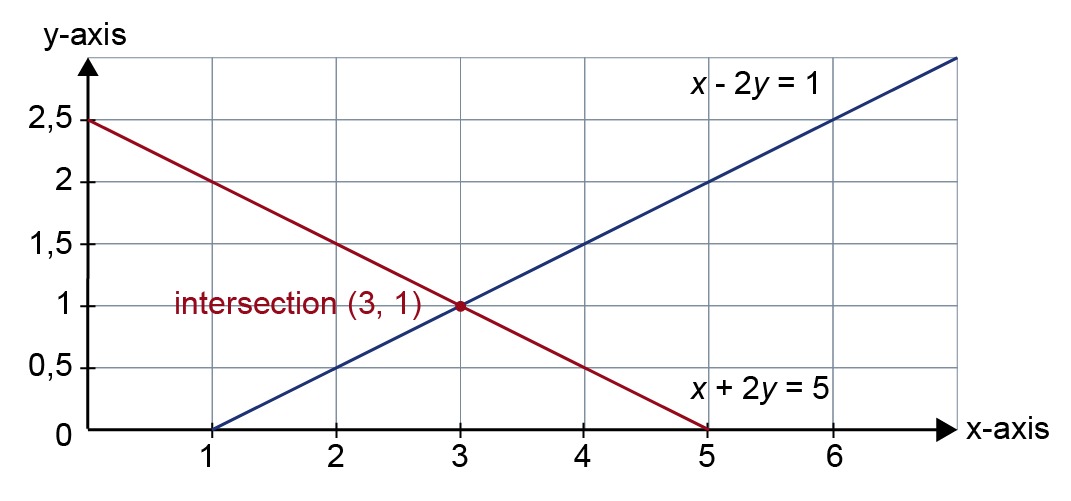
Answer: The solution of the pair of equations is [[$ x = 3 $]]​ and [[$ y = 1 $]]​.