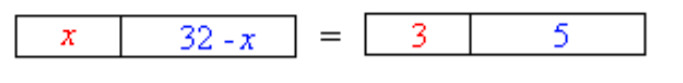Proportions can be also be used to compare quantities in different units. For example, if [[$ 3 $]] kg of strawberries costs € [[$ 5 \: $]], then [[$ 15 $]] kg of same strawberries will cost € [[$ 25 \: $]]. The ratio between the quantity and price of strawberries therefore remains the same.

[[$ \displaystyle\frac {3 \: \text {kg}} {5 \: \text {€}} = \displaystyle\frac {15 \: \text {kg}} {25 \: \text {€}} $]]​

In proportions, colons are often used to signify division. The quantities of proportions are named as follows:

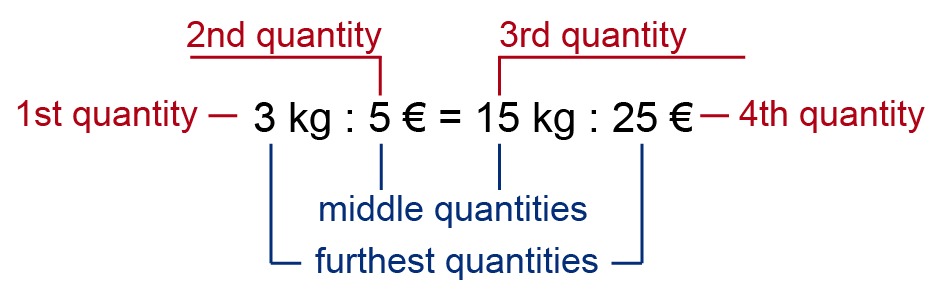
A special feature of proportion equations is that the product of its furthest quantities is equal to the product of its middle quantities. This can be achieved with a process called cross multiplying, as seen below:

If three quantities of a proportion equation are known, the fourth unknown can solved with cross multiplication. After this, the equation can be solved according to the familiar equation-solving rules.

Example 1

Solve the proportions.

a) [[$ \displaystyle\frac {x} {6} = \displaystyle\frac {2} {3} $]]​

b) [[$ \displaystyle\frac {5} {x} = \displaystyle\frac {10}{6} $]]

Solution:

a)		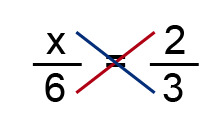Cross-multiplication is applied.
	[[$ \quad \begin{align} 3x &= 6 · 2 \ \\ 3x &= 12 \space ||:3 \ \\ x &= 4 \end{align} $]]​

b)		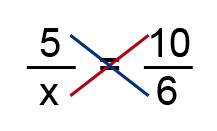Cross-multiplication is applied.
	[[$ \quad \begin{align} 5 · 6 &= 10x \ \\ 30 &= 10x \ \\ -10x &= -30 \space ||:(-10) \ \\ x &= 3 \end{align} $]]​

Example 2

Divide € [[$ 32 $]]​ in a ratio of [[$ 3 : 5 $]]​ using a proportion equation.



[[$ \quad \begin{align} \dfrac{x}{32 - x} &= \dfrac{3}{5} \ \\ 5x &= 3(32 - x) \ \\ 5x &= 96 - 3x \ \\ 5x + 3x &= 96 \ \\ 8x &= 96 \space ||:8 \ \\ x &= \dfrac{96}{8} x &= 3 \end{align} $]]​


The first part is [[$ 12 $]]​, whereas the other part is [[$ 32 –12 = 20 $]]​.

Answer: The parts are [[$ 12 \: \text € $]]​ and [[$ 20 \: \text € $]]​.