If two lines travelling on a plane are not parallel to one another, they will inevitably intersect at some point. The coordinates of the point of intersection are found when the lines are drawn in the same coordinate system.

Example 1

Determine the intersections of the line [[$ y = \: –2x \: – 2 $]]​ and the coordinate axes by drawing the line in a coordinate system.

Solution: Calculate a few values of [[$ y $]] with a few values of [[$ x $]], place the obtained points in the coordinate system and draw a line through them.

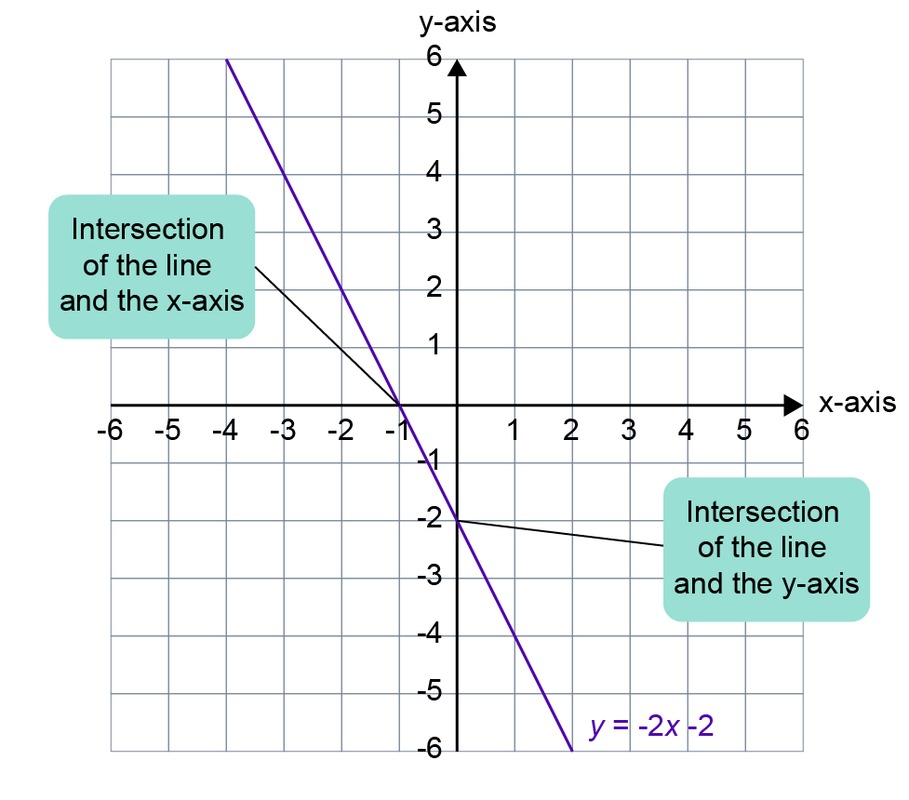
[[$ x $]]​	[[$ y = \:–2x \: – 2 $]]​	[[$ (x, y) $]]​
[[$ -1 $]]​	[[$ –2 \cdot (–1) \:– 2 = 0 $]]​	[[$ (–1, 0) $]]​
[[$ 0 $]]​	[[$ –2 \cdot (0) \:– 2 = 0 $]]​	[[$ (0, –2) $]]​
[[$ 1 $]]​	[[$ –2 \cdot (1) \: – 2 = 0 $]]​	[[$ (1, –4) $]]​

Answer: The line intersects the [[$ x $]] axis at [[$ (-1, 0) $]] and the [[$ y $]] axis at [[$ (0, -2) $]].

NB! The solution [[$ x = \: –1 $]] of the equation [[$ –2x \: - 2 = 0 $]] can be found in the intersection of the line [[$ y = \: - 2x \: - 2 $]] and the [[$ x $]] axis.

Example 2

Solve the equation [[$ 4x \:– 7 = 2x \: – 1 $]]​ by drawing.

First, simplify the expression [[$ 4x \: - 7 = 2x \: - 1 $]] by bringing all of its terms to the left side of the equation.

[[$ \begin{equation} \begin{split} 4x \: – 7 & = 2x \: – 1 \\ 4x \: – 7 \: – 2x + 1 & = 0 \\ 2x \: – 6 & = 0 \\ \end{split} \end{equation} $]]​

Then, draw the line [[$ y = 2x \: - 6 $]] in the coordinate system.

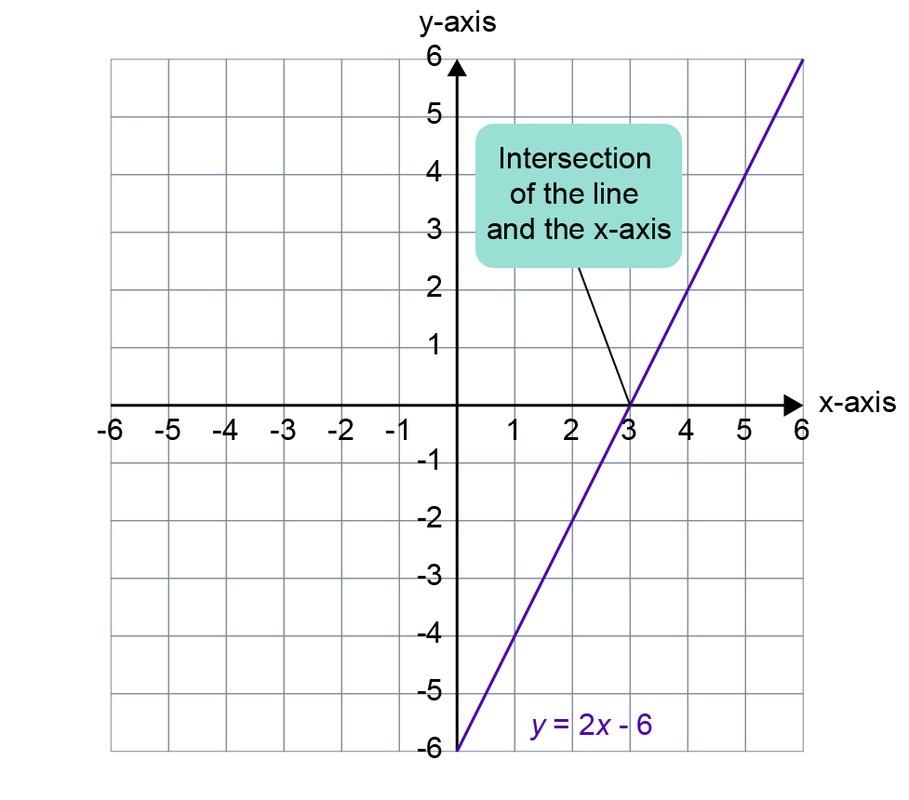
[[$ x $]]​	[[$ y = 2x \: – 6 $]]​	[[$ (x, y) $]]​
[[$ 0 $]]​	[[$ 2 \cdot 0 \: – 6 = \: –6 $]]​	[[$ (0, –6) $]]​
[[$ 2 $]]​	[[$ 2 \cdot 2 \: – 6 = \: -2 $]]​	[[$ (2, –2) $]]​
[[$ 4 $]]​	[[$ 2 \cdot 4 \: – 6 = 2 $]]​	[[$ (4, 2) $]]​

Answer: The solution of the equation can be found at the intersection of the line and the [[$ x $]] axis: [[$ x = 3 $]].

Example 3

Define the point at which the lines [[$ y = \displaystyle\frac {1} {2}x \: – 1 $]]​ and [[$ y = \: –x + 5 $]] intersect by drawing​.

First, draw the lines [[$ y = \displaystyle\frac {1} {2}x \: – 1 $]]​ and [[$ y = \: –x + 5 $]]​ in the same coordinate system.

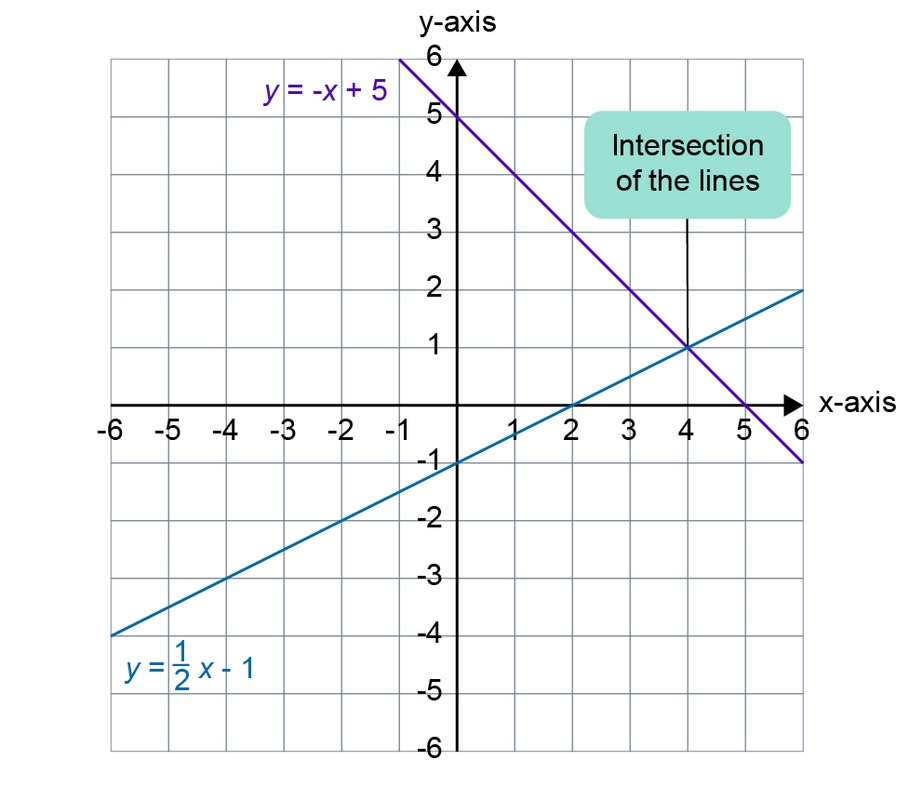
[[$ x $]]​	[[$ y = \displaystyle\frac {1} {2}x \: – 1 $]]​	[[$ (x, y) $]]​
[[$ –2 $]]​	[[$ \displaystyle\frac {1} {2} \cdot (–2) \: – 1 = \: –2 $]]​	[[$ (–2, –2) $]]​
[[$ 0 $]]​	[[$ \displaystyle\frac {1} {2} \cdot 0 \: – 1 = \: -1 $]]​	[[$ (0, –1) $]]​
[[$ 2 $]]​	[[$ \displaystyle\frac {1} {2} \cdot 2 \: – 1 = 0 $]]​	[[$ (2, 0) $]]​

[[$ x $]]​	[[$ y = \: –x + 5 $]]​	[[$ (x, y) $]]​
[[$ 0 $]]​	[[$ –0 + 5 = 5 $]]​	[[$ (0, –6) $]]​
[[$ 1 $]]​	[[$ –1 + 5 = 4 $]]​	[[$ (2, –2) $]]​
[[$ 2 $]]​	[[$ –2 + 5 = 0 $]]​	[[$ (4, 2) $]]​

Answer: The coordinates of the point at which the lines intersect are [[$ (4, 1) $]].