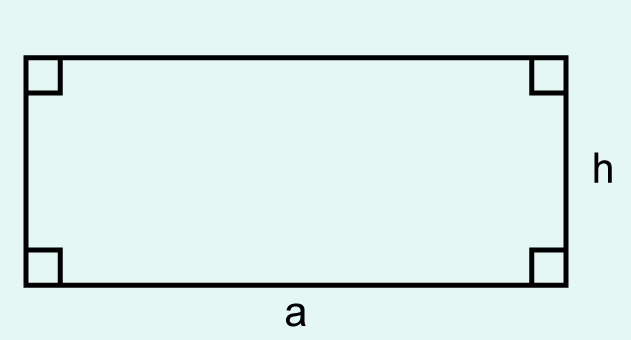
The area of a rectangle is the product of its base and altitude:

[[$ A = a \cdot h $]]

Note! Since the altitude and the base of a rectangle converge, the area of the rectangle can also be calculated as the product of two adjacent sides.

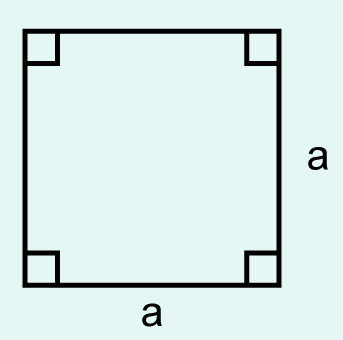
The area of a square is the product of its base and altitude, i.e. the product of two adjacent sides:

[[$A = a \cdot a = a^2$]]

Note! The base and altitude of the square are equal in length.

Example 1

Calculate the area of the tatami mat.

The mat is a rectangle, which means that

[[$ A = a\cdot h = \text{180.0 cm} \cdot \text{90.0 cm} = 16 200 \text{ cm}^2 $]]

The value of 16200 is quite big, so it would be more illustrative to give an answer using a bigger area unit. How do you convert 16200 cm² to square metres?

Units of area

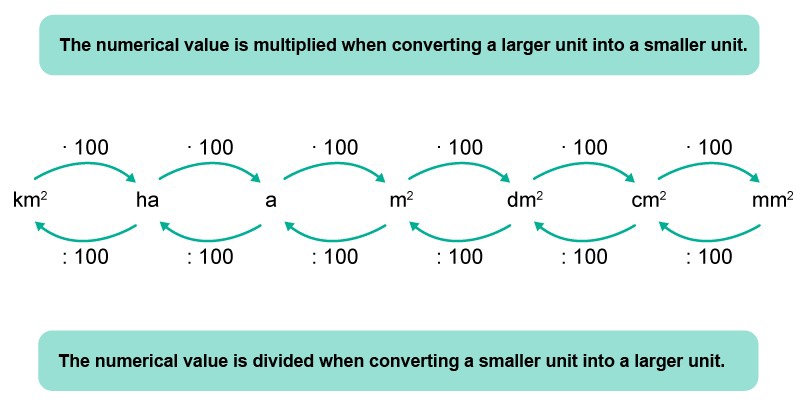
Since the ratio for units of length in the SI system is ten, the ratio for units of area [[$ \text{m}^2 = \text{m} \cdot \text{m} $]] must be [[$10\cdot10 = 100$]]. The table shows the most common units of area.

Symbol	Name	In basic units
km²	square kilometre	1 000 000 m²
ha	hectare	10 000 m²
a	are	100 m²
m²	square metre	1 m²
dm²	square decimetre	0,01 m²
cm²	square centimetre	0,0001 m²
mm²	square millimetre	0,000001 m²

As with lengths, a smaller unit can be converted into a larger one by dividing its numerical value by the ratio. Conversely, a larger unit can be converted into a smaller unit by multiplying its numerical value by the ratio.

Example 2

Convert:

a) [[$ \text{3,2} $]] square kilometres to hectares.

[[$\begin{align} \text{3,2 km}^2 = 100 \cdot \text{3,2 ha} = \text{320 ha} && \text{Convert to one unit smaller.} \end{align}$]]

b) [[$ 16200 $]] square centimetres to square metres.

[[$\begin{align} 16200 \text{ cm}^2 = \dfrac{16200}{100 \cdot 100} \text{ m}^2 = \text{1,62 m}^2 && \text{Convert to two units greater.} \end{align}$]]

Like in length unit conversions, we can take advantage of the knowledge that the number notation system we use is decimal and has a base number of [[$10$]]. Since the area unit conversion ratio is [[$100$]], each unit conversion always moves the decimal point by two steps.

Example 3

Convert the areas a) [[$240$]] mm² and b) [[$\text{3,2}$]] ha to square metres.