Aaltoilmiöitä

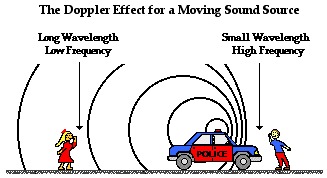
Dopplerin ilmiö

  • Äänen taajuuden riippuvuutta äänilähteen ja havainnoijan välisestä nopeudesta kutsutaan Doppler-ilmiöksi.
  • Esim. kun ambulanssi lähestyy sen ääni kuulostaa kimeämmältä kuin sen loitotessa.
  • Kun aaltoliikkeen nopeus väliaineessa on v ja taajuus f0, ja äänilähteen etääntymisnopeus suhteessa havainnoijaan on v1, saadaan havaittu taajuus f seuraavasti [[$$ f = f_0 {v \over v \pm v_1} $$]]​
  • Etääntymisnopeus on negatiivinen, kun äänilähde lähestyy havainnoijaa.


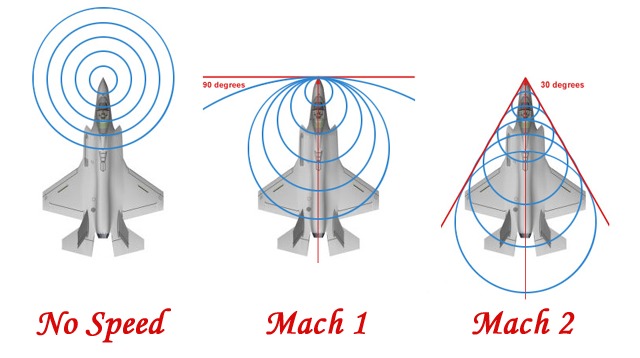
  • Kun kappaleen nopeus väliaineessa ylittää äänen nopeuden syntyy niin sanottu kiila-aalto.

Seisova aaltoliike

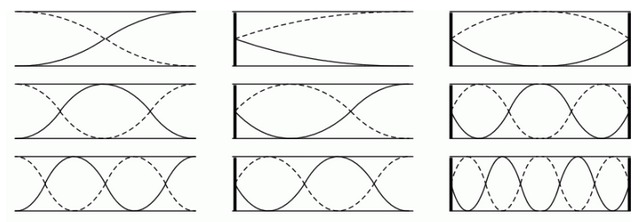
Seisovat aallot
  • On aaltoliikettä, joka ei liiku.
  • Syntyy kappaleeseen tai äärelliseen tilaan (esim. kitaran kieli).
  • Tilassa heijastuvat aallot vahvistavat ja kumoavat toisiaan (eli interferoivat) siten, että vain kyseisen tilan ominaisvärähtelytaajuudet jäävät jäljelle.
  • Värähtelymaksimin nimi on kupu ja minimin solmu.
  • Solmu syntyy tilan reunalle. Jos jokin reuna on auki (seinämä puuttuu), syntyy sinne kupu.
  • Ominaisvärähtelytaajuuksia on useita. Alinta taajuutta kutsutaan perustaajuudeksi. Lisäämällä kupuja aina yhdellä, saadaan ylitaajuuksia vastaavat aaltomuodot.
Alla olevassa kuvassa on esitelty värähtevän tilan kolme eri muotoa, vasemmalta oikealle:
  1. Tilan kummatkin päät auki,
  2. toinen pää auki ja toinen kiinni,
  3. kummatkin päät kiinni.
Ylin edustaa perustaajuutta, alemmat ylätaajuuksia.




Äänen intensiteetti

  • Äänen voimakkuus on kääntäen verrannollinen suhteessa etäisyysteen äänilähteestä.
  • Äänilähteestä lähtevä ääni laajenee ilmapallon tavoin. Pinta-alan kasvaessa teho pinta-alayksikköä kohden pienenee.
  • Esim. Lasketaan paineiden suhde, kun etäisyys äänilähteestä kolminkertaistuu
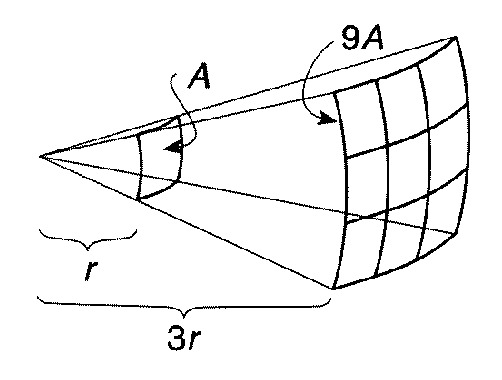​[[$$ A_1 = 4 \pi r^2 $$]]​[[$$ A_2 = 4 \pi (3r)^2 = 4 \pi 9 r^2 = 9 A_1 $$]]​[[$$ P_1 = {P \over A_1} $$]]​[[$$ P_2 = {P \over 9 A_1} = {1 \over 9} \cdot P_1 $$]]​

Äänen intensiteetti

  • Lasketaan äänilähteen tehon P ja pinta-alan A avulla​[[$$ I = {P \over A} $$]]​
  • Yksikkö on wattia neliömetriä kohden [I] = W/m2.
  • Ihmiskorva erottaa juuri ja juuri äänen (kun taajuus on 1000 Hz), jonka intensiteetti on [[$$ I_0 = 10^{-12} {W \over m^2} $$]]​.
  • Äänen voimakkuus ilmaistaan intensiteettitasona L, jonka yksikkö on desibeli dB.[[$$ L = 10 \log_{10} \bigg[ {I \over I_0} \bigg] dB $$]]​
  • Äänen intensiteetti kymmenkertaistuu desibelien kasvaessa kymmenellä. Eli 80 dB äänen intensiteetti on 100-kertainen suhteessa 60 dB ääneen.
  • Ihmiskorva aistiin äänen voimakkuuden kaksinkertaistuvan desibelien kasvaessa kymmenellä.
  • Kun puhutaan äänen voimakkuudesta, tulee olla tarkka: tarkoitetaanko sillä intensiteettiä, vai sitä miten ihminen aistii äänen?
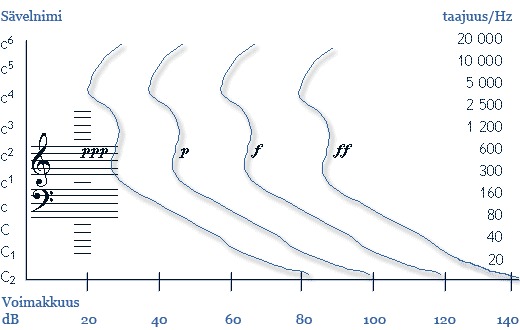
  • Oheinen kaavio kuvaa miten äänen voimakkuuden aistiminen riippuu taajuudesta.