Sähköstatiikka
9 Sähkövaraus
Sähkövaraus
Sähköinen vuorovaikutus
- Kaikki aine koostuu varatuista hiukkasista protoneista ja elektroneista (sekä neutroneista).
- Lähtökohtaisesti protoneja ja elektroneja on sama määrä, joten ulospäin aine näyttäytyy sähköisesti neutraalilta.
- Käytännössä aineessa on usein varaus, eli se sisältää enemmän joko positiivisia tai negatiivisia varauksia.
- Epätasapaino syntyy, kun systeemille tehdään työtä (mekaanista, tai kemiallista). Työ, eli energia erottelee negatiiviset varaukset positiivisista.
- Varautuneet hiukkaset ovat elektroneja tai ioneja, eli varautuneita molekyylejä.
- Jos varatut hiukkaset pääsevät liikkumaan (kuten vapaat elektronit) voi tapahtua sähköpurkauksia (esim. salama).
Sähköinen vuorovaikutus
- Sähköinen vuorovaikutus selittää suurimman osan arkipäivän ilmiöistä. Esimerkiksi kosketusvoimat perustuu molekyylien väliseen sähköiseen vuorovaikutukseen.
- Varaukset ovat sähköisessä vuorovaikutuksessa toisten varausten kanssa.
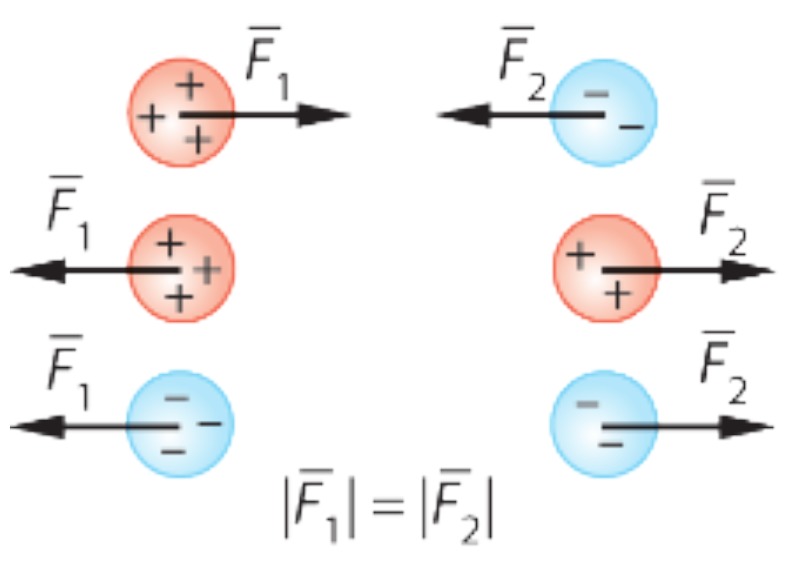
- Jos varaukset ovat erimerkkisiä ne vetävät toisiaan puoleensa. Tämä johtuu siitä, että varaukset pyrkivät aina tasoittumaan kohti nollavarausta.
- Saman merkkisesti varaukset hylkivät toisiaan.
- Makrotasolla sähköinen vuorovaikutus ilmenee varautuneiden kappaleiden välisinä sähköisinä voimina.
- Varauksen symboli on Q ja yksikkö on coulumbi C.
- Yhden elektronin varaus on hyvin pieni [[$ e = 1,602 \cdot 10^{-19} C$]]
- Akuissa varaus ilmaistaan ampeeritunteina Ah tai milliampereeritunteina mAh.
- Selvitä miten sähköiset varaukset syntyvät luonnossa.
- Missä käytännön ilmiöissä sähköinen vuorovaikutus ilmenee?
- Mitä ovat ionit ja miten ioneita merkitään?
- Muuta varaus coulombeista alkeisvarauksiksi ja päin vastoin.
10 Sähköinen voima ja Coulombin laki
Coulumbin voima
 Eristeen vaikutus sähköiseen voimaan
Eristeen vaikutus sähköiseen voimaan
Tehtäviä
- Sähköinen voima on suoraanverrannollinen varauksen suuruuteen.
- Etäisyys heikentää voimaan suhteessa toiseen potenssiin. (Ajattele pallokuori, joka laajenee).

- Coulombin laki ilmaisee kahden pistemäisen varauksen välisen voiman tyhjiössä:
- kaavassa k on Coulumbin lain vakio [[$ k = 8,9876 \cdot 10^9 \frac{Nm^2}{C^2} $]].
- Kahden kappaleen toisiinsa kohdistamat sähköiset voimat ovat aina keskenään yhtäsuuret, mutta vastakkaissuuntaiset.

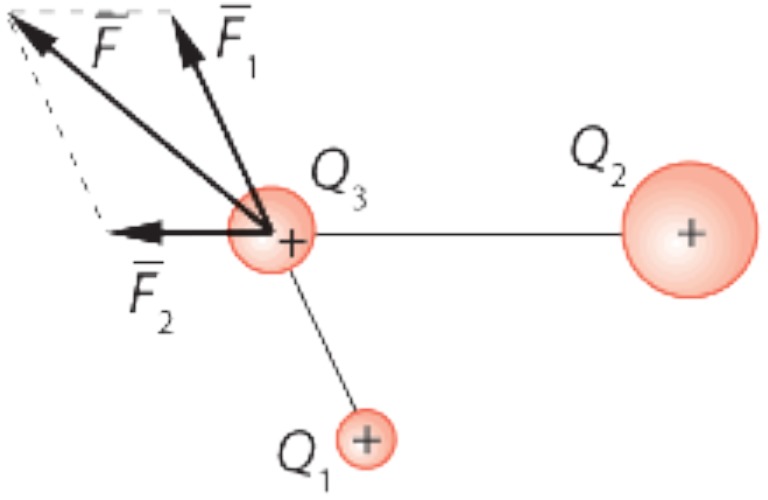
- Jos kappaleeseen kohdistuu useampia voimia, tulee ne laskea vektoriopin mukaisesti vektorisummana.
 Eristeen vaikutus sähköiseen voimaan
Eristeen vaikutus sähköiseen voimaan- Jos varauksien välillä on eriste, se heikentään sähköistä vuorovaikutusta. Tämä johtuu sähköisestä influenssista.
- Eriste on kappale, jossa ei ole vapaita varauksenkuljettajia (esim. eristysteippi tai tislattu vesi).
- Heikennyksen voimakkuus riippuu eristeen suhteellisesta permittiivisyydestä [[$ \epsilon_r $]].
- Coulombin laki saa nyt muodon:
Tehtäviä
- Laske kahden varauksen välillä vaikutta sähköinen voima.
- Piirrä vektorisumma, kun varaukseen vaikuttaa kaksi tai useampi erisuuruinen voima.
- Laske vektorisumma, kun varaukseen vaikuttaa kaksi tai useampi erisuuruinen voima.
- Tarkastele eri aineiden suhteellista permittiivisyyttä.
- Laske elektronin kiihtyvyys tyhjiössä, kun metrin päässä siitä on yhden coulombin varaus.
11 Sähkökenttä
Sähkökenttä
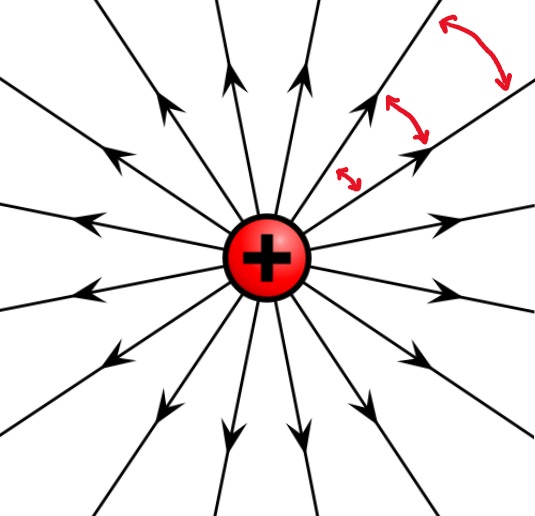
Kenttäviivat
Sähköinen influenssi
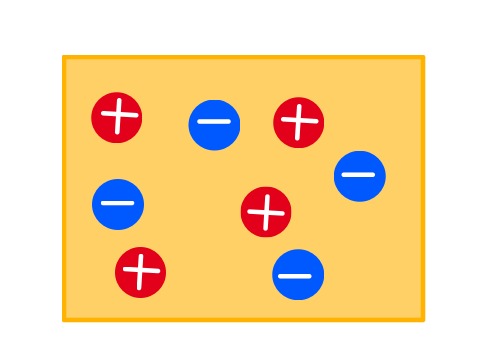 KUVA2: Kytketään ulkoinen sähkenttä päälle.
KUVA2: Kytketään ulkoinen sähkenttä päälle.
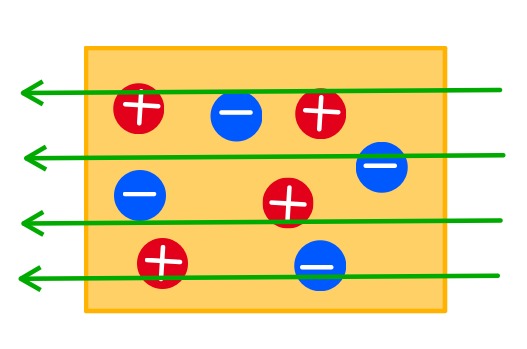 KUVA3: Ulkoisen sähkökentän vaikutuksesta varaukset siirtyvät kappaleen reunoille ja luovat sisäisen sähkökentän.
KUVA3: Ulkoisen sähkökentän vaikutuksesta varaukset siirtyvät kappaleen reunoille ja luovat sisäisen sähkökentän.
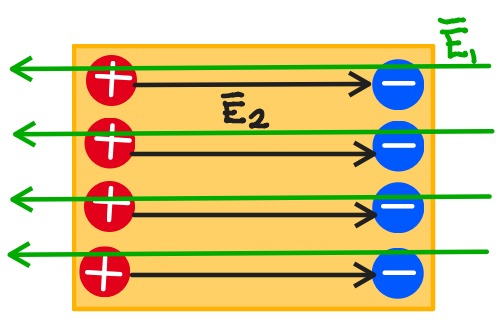
KUVA4: Ulkoinen ja sisäinen sähkökenttä kumoavat toisensa, siten että johteen sisällä sähkökenttä on nolla.
 Tehtäviä
Tehtäviä
- Sähkökenttä on teoreettinen käsite, jolla havainnollistetaan sähköistä vuorovaikutusta.
- Varausten ympärillä on sähkökenttä, joka vaikuttaa muihin varauksiin.
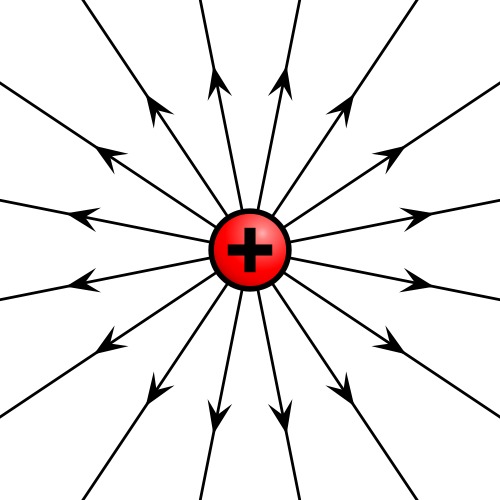
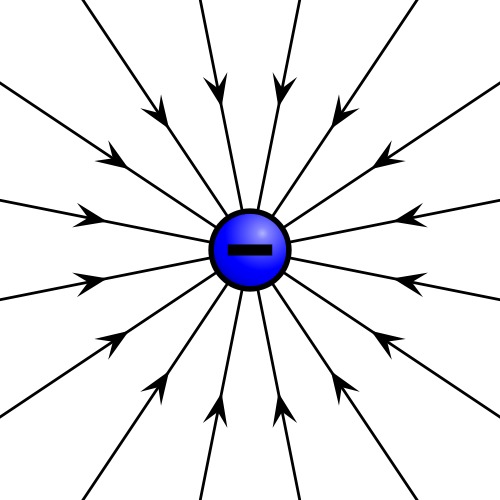
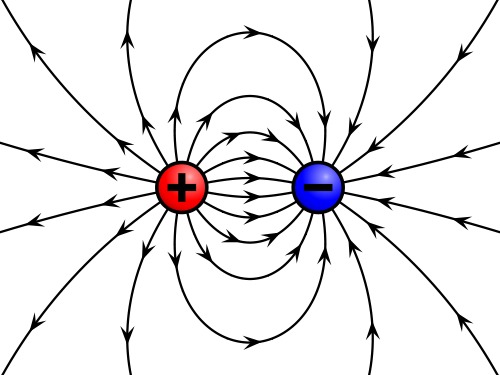
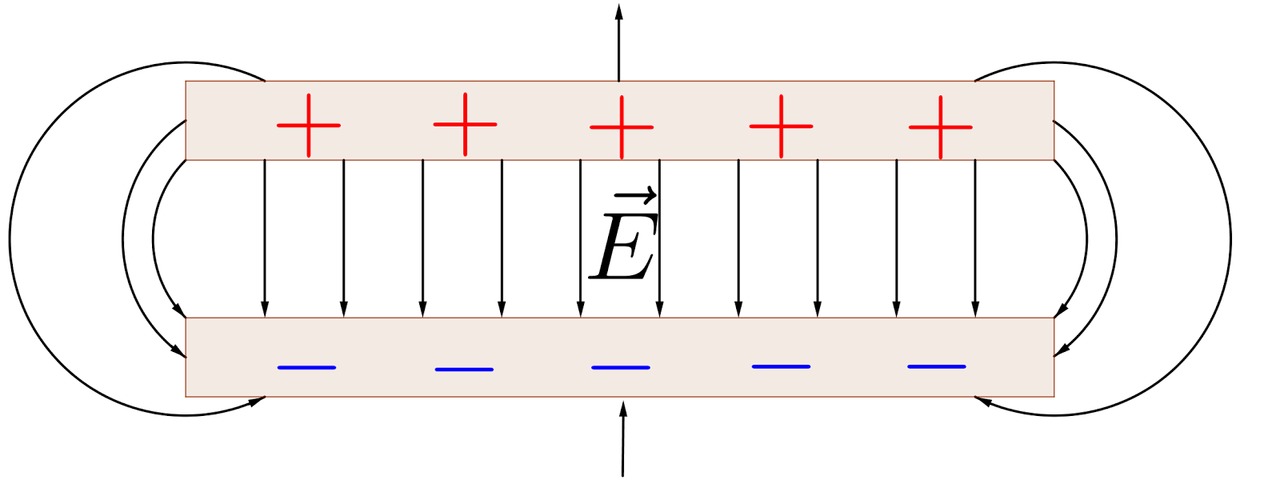
- Sähkökenttää havainnollistetaan piirtämällä kenttäviivojen avulla.
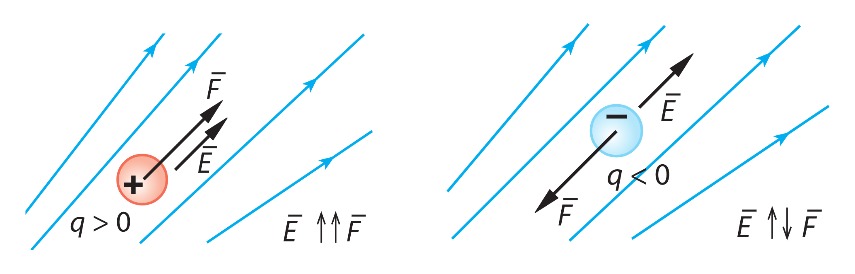
- Sähkökenttä on vektorisuure, jonka symboli on E ja yksikkö on N/C (newton/coulombi).
- Sähkenttä saadaan jakamalla varaukseen kohdistuva voima F kentässä olevan varauksen suuruudella q.
- Pistemäiselle varaukselle kentän voimakkuus saadaan Coulombin laista:
Kenttäviivat
- Kenttäviivojen nuolet osoittavat positiiviseen varaukseen kohdistuvat voiman suuntaan.

- Kenttäviivojen tiheys osoittaa kentän voimakkuutta. Mitä tiheämmässä nuolet ovat sitä voimakkaampi kenttä on.




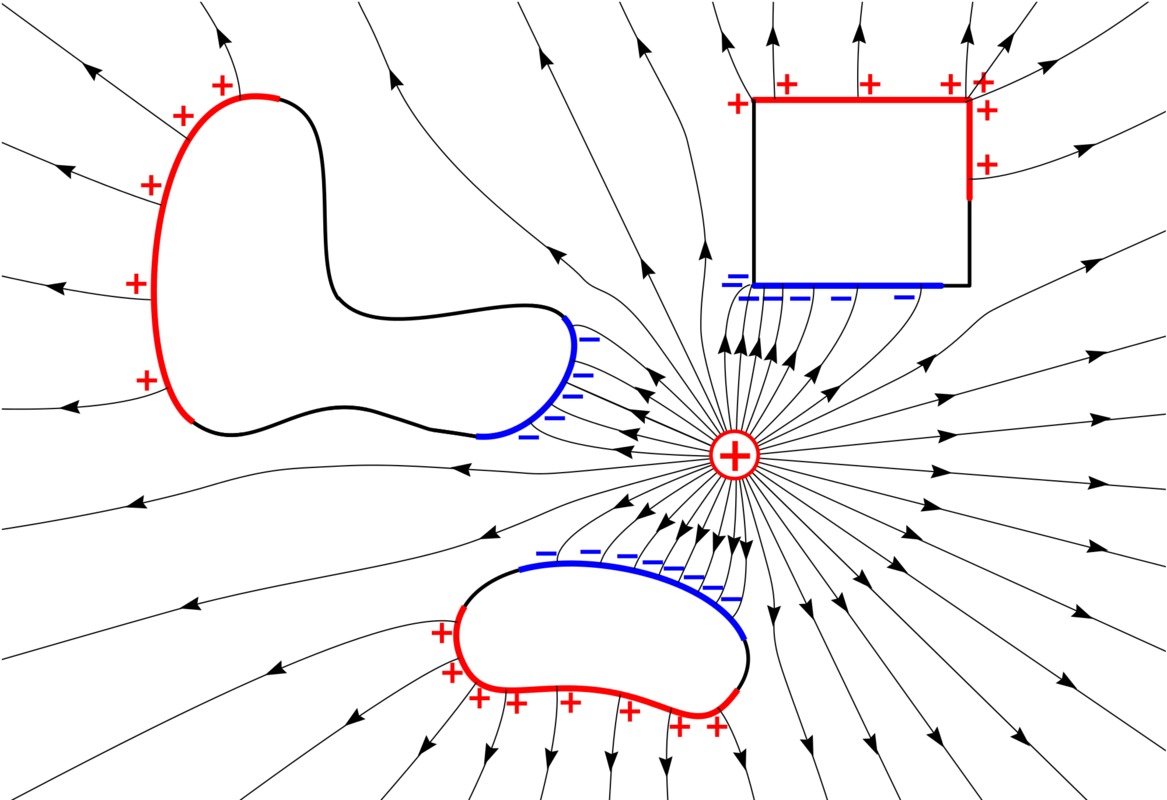
Sähköinen influenssi
- Sähkökenttä vaikuttaa aineeseessa oleviin varauksiin. Tätä kutsutaan sähköiseksi influensseksi.
- Johdekappaleessa sähköiset varaukset liikkuvat sähkökentän suuntaisesti vastakkaisille reunoille.
- Tämä aiheuttaa johteen sisäisen sähkökentän, joka kumoaa täysin ulkoisen sähkökentän. Johteen sisällä sähkökentän suuruus on nolla.
 KUVA2: Kytketään ulkoinen sähkenttä päälle.
KUVA2: Kytketään ulkoinen sähkenttä päälle. KUVA3: Ulkoisen sähkökentän vaikutuksesta varaukset siirtyvät kappaleen reunoille ja luovat sisäisen sähkökentän.
KUVA3: Ulkoisen sähkökentän vaikutuksesta varaukset siirtyvät kappaleen reunoille ja luovat sisäisen sähkökentän.
KUVA4: Ulkoinen ja sisäinen sähkökenttä kumoavat toisensa, siten että johteen sisällä sähkökenttä on nolla.

- Eristeessä varaukset eivät pääse vapaasti liikkumaan.
- Eristeessä dipoliset molekyylit kääntyvät kentän suuntaiseksi luoden sähkökentän, joka osittain kumoaa ulkoisen sähkökentän.
- Vaikkei aineessa olisikaan dipolisia molekyylejä, sähkenttä saa molekyylit dipolisoitumaan.
 Tehtäviä
Tehtäviä- Mistä sähkentät syntyvät?
- Miten sähkenttä vaikuttaa eristeeseen ja miten johteeseen?
- Laske sähkentän suuruus pistevaraukselle etäisyydellä x varauksesta.
- Piirrä pistevarauksen sähkenttä.
- Piirrä kahden pistevarauksen luoma sähkökenttä.
- Laske sähkökentän aiheuttama voima ja kiihtyvyys elektronille.
12 Homogeeninen sähkökenttä
Homogeeninen sähkökenttä
Tehtäviä
- Sähkökenttää kutsutaan homogeeniseksi, kun sen suunta ja voimakkuus on vakio.
- Homogeeninen sähkökenttä saadaan aikaiseksi kahdella yhdensuuntaisella levyllä, joiden välille on kytketty jännite.

- Homogeenisiä sähkökenttiä hyödynnetään monella tavalla erilaisissa sähkölaitteissa.
- Missä tahansa sähkökentässä voidaan laskea potentiaaleja, mutta homogeenisessa kentässä se on erityisen helppoa.
- Potentiaali virtapiireissä on täsmälleen sama asia kuin potentiaali sähkökentissä. Virtapiireissä nimenomaan jännitteen aiheuttama sähkökenttä saa virran aikaiseksi.
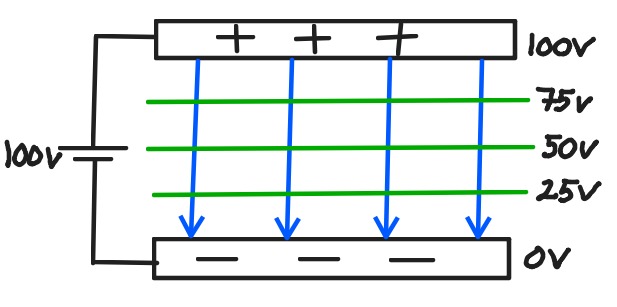
- Alueita, joissa potentiaali on sama kutsutaan tasapotentiaalipinnoiksi.
- Nollapotentiaaliksi valitaan yleensä negatiivinen levy.
- Tällöin positiivisen levyn potentiaali on sama kuin levyjen välinen jännite.
- Muuten potentiaali muuttuu tasaisesti levyjen välissä. Puolivälissä se on puolet jännitteestä jne.

- Sähkökenttään E ja potentiaaliin V liittyvät laskut tehdään seuraavan kaavan avulla. Tässä x on kohtisuora etäisyys negatiivisesta levystä.
Tehtäviä
- Mikä on homogeeninen sähkökenttä?
- Piirrä homogeeninen sähkökenttä ja siihen tasapotentiaaleja.
- Laske potentiaaleja kentän eri kohdissa.
- Määritä sähkökentän voimakkuus, kun tunnetaan jännite-ero ja levyjenvälinen etäisyys.
- Laske tapauksia, joissa levyjä on useampia. Esim. 12-7.
13 Varattu kappale sähkökentässä
Varattuun kappaleeseen sähkökentässä
Kappale liikkuu poikittain sähkökentän suhteen
- Varattuun kappaleeseen, jonka varaus on q, vaikuttaa sähkökentässä sähköinen voima.
- Jos kappaleeseen ei vaikuta muita voimia, voidaan kiihtyvyys laskea seuraavasti.
- Homogeenisessa sähkökentässä voiman suunta ja suuruus pysyvät vakiona, mikä helpottaa kappaleen liikkeen laskemista.
- Sähköinen voima vaikuttaa liikkeen suuntaan tai sitä vastaan. Kiihtyvyys tapahtuu yhdessä suunnassa ja laskut ovat helppoja.
Kappale liikkuu poikittain sähkökentän suhteen
- Voima vaikuttaa kohtisuorasti kappaleen liikesuuntaa vastaan.
- Jos muita voimia ei vaikuta, kappaleen liikesuunta ja vauhti alkavat muuttumaan sähköisen voiman vaikutuksesta.