Mekaaninen aaltoliike

Mekaaninen värähtelijä

• Värähtelijä ja aaltoliikkeen synty
• Mekaaninen värähtelijä, jousivakio ja harmoninen voima [[$ F = - kx $]]​.
• Muista, että harmonisen voiman suunta on aina värähtelykeskipistettä kohti.
• Harmonisen mekanisen värähtelijän jaksonaika [[$ T = 2 \pi \sqrt{m \over k} $]]​
• Värähtelyn perusominaisuudet: nopeus v, taajuus f, jaksonaika T, amplitudi A
• Värähtelyn vaimeneminen

Aaltoliike

• Aaltoliikkeen perusominaisuudet: aallon etenemisnopeus v, aallonpituus [[$ \lambda $]]​, jaksonaika T, taajuus f, amplitudi A ja kahden aallon välinen vaihe-ero [[$ \phi $]]​.
• Osaa lukea yo. ominaisuudet kuvaajasta. Osaa piirtää harmoninen aalto (sin-aalto).
• Aaltoliikkeen perusyhtälö [[$ v = \lambda f $]]​ ja [[$ f = {1 \over T} $]]​
• Vaimenee suhteessa etäisyyden neliöön [[$ I \sim {1 \over r^2} $]]​ (ilmapallo-efekti).
• Aaltojen interferenssi, eli yhteisvaikutus. Samantaajuiset aallot voivat vahvistaa tai heikentää toisiaan vaihe-erosta riippuen.
• Huygensin periaate: jokainen aaltorintaman piste on uuden ympyrä-aallon lähde.
• Taipuminen esteen lähellä, eli diffraktio selitetään Huygensin periaatteella.
• Taittuminen tapahtuu kahden aineen rajapinnassa. Taittumisessa taajuus säilyy.
• Taittumislaki [[$ { \sin{\alpha_1} \over \sin{\alpha_2}} = { v_1 \over v_2} = n_{12} $]]​
• Heijastuskulma aina sama kuin tulokulma.
• Kokonaisheijastuminen, kun taitekulma on 90 astetta (tai enemmän). Tapahtuu vain kun v₂ > v₁, esim. ääni ilmasta veteen.

Mekaaninen aaltoliike

• Mekaaninen aaltoliike on väliaineessa etenevä häiriö.
• Poikittainen värähtely vain kiinteässä aineessa, pitkittäinen myös fluideissa.
• Pulssin heijastuessa tiheämmästä aineesta, vaihe muuttuu vastaiseksi. Heijastus harvemmasta säilyttää vaiheensa.
• Seisova aalto, kuvut ja solmut, ominaistaajuudet, resonanssi ja ylävärähtely.
• Solmu syntyy kammion päähän, kun vastassa tiheämpi aine, kupu muuten.
• Ylävärähtelysarja, osaa laskea taajuudet:
• 

Ääniaallot

• Ääniaalloilla on kaikki aaltoliikkeen ominaisuudet
• Väliaineen lämpötilan vaikutus äänen nopeuteen [[$ v_2 = v_1 \sqrt{ T_2 \over T_1} $]]​, eli nopeus on verrannollinen tämpötilan neliöjuureen.
• Huojunta, kun aallonpituudet lähellä toisiaan. Huojuntataajuus [[$ f = | f_1- f_2| $]]​.
• Äänen intensiteetti I on äänen tehon P määrä pinta-ala yksikköä kohden. [[$ I = {P \over A}$]]​. Yksikkö[[$ [ I ] = 1 {W \over m^2} $]]​.
• Intensiteettitaso L ilmaistaan desibeleinä [[$ L = 10 \log {I \over I_0} dB $]]​. Missä I₀ = 10^-12 W/m² on kuulokynnys, eli heikoin ääni mitä ihminen kuulee. Kun desibelit kasvavat kymmenellä, intensiteetti kymmenkertaistuu. Ihminen aistii 10 dB muutoksen äänen voimakkuuden kaksinkertaistumisena.
• Ihminen aistii äänen taajuuksia noin välillä 20 Hz - 20 kHz. Taajuus vaikuttaa havaintoon äänen voimakkuudesta.
• Yli 1000 MHz ääni kutsutaan ultraääniksi. Ultraäänien sovellukset.
• Dobblerin ilmiö esiintyy, kun äänilähde on liikkeessä suhteessa äänen kuulijaan. Havaittu taajuus [[$ f= f_0 { v \over v \pm v_1 } $]]​, missä v on äänen nopeus ja v₁ on suhteellinen liikkeen nopeus. Merkki on positiivinen, kun äänilähde loittonee.
• Yli äänen nopeudella liikkuvat kappaleet synnyttävät kiila aallon.

Valoaallot

• Valoaalloilla on kaikki aaltoliikkeen ominaisuudet.
• Se on sähkömagneettista etenemissuunnan kanssa poikittaista värähtelyä, joka etenee tyhjiössä nopeudella c = 300 000 km / s.
• Väliaineessa valo etenee hitaammin.
• Sähkökenttä ja magneettikenttä värähtelevät poikittain toistensa suhteen.
• Värähtelyn suunnanksi on sovittu sähkökentän suunta.
• Kun värähtelyä tapahtuu vain yhdessä suunnassa valo on täysin polarisoitunutta.
• Polarisaatiota tapahtuu mm. suositimissa kuten aurinkolaseissa ja valon heijastuessa aineiden rajapinnasta.
• Brewsterin lain mukaan valo on täysin polarisoitunutta, kun taitekulman ja heijastuskulman välinen kulma on tasan 90 astetta. Polarisaatio tapahtuu kun saapuvan valon kulman tangentti on aineiden taitekertoimien osamäärä: [[$ \tan \alpha_p = {n_2 \over n_1} $]]​.
• Näkyvän valon aallonpituus on noin 400 nm - 700 nm.
• Yksiväristä valoa (valoa, jossa esiintyy vain yhtä aallonpituutta) kutsutaan monokromaattiseksi valoksi.
• Dispersio: eri aallonpituuksiset valot etenevät eri nopeudella väliaineessa. Dispersion seurauksena auringonvalo hajoaa (dispersoituu) prismassa eri väreiksi (monokromaattinen valo ei hajoa).
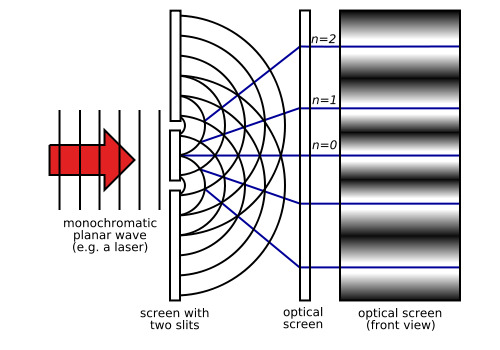
• Kaksoisaukko kokeessa samanvaiheiset ja aallonpituuksiset valonsäteen johdetaan kahdesta hyvin lähekkäin olevasta aukosta. Tapahtuu hyugensin periaatteen mukainen valon taipuminen. Kun kahdesta aukosta tulleet säteet kohtaavat, ne interferoivat ja syntyy interferenssikuvio, jota voidaan tarkastella esim. varjostinkankaalla. Kuviossa näkyy kirkkaana pistemäiset alueet, jossa valonsäteet vahvistavat toisiaan.
• Valon taipuminen lasketataan kaavalla: [[$ d \sin \alpha = k \lambda, k = 0, 1, 2, ... $]]​. Nollanen kertaluvun valomaksimi syntyy varjostimelle aukkojen keskikohtaan. Muut kertaluvut kummallekin puolelle aukkoja.
• 
• Hila on kappale, jossa on tiheästi lukuisia aukkoja vakioetäisyydellä toisistaan. Valo käyttäytyy hilassa kuten kaksoisaukossa, mutta varjostimelle syntyvä kuvio on selkeämpi ja kirkkaampi.

Geometrinen optiikka

• Valonsäteet etenevät suoraviivaisesti (paitsi avaruudessa voimakkaissa painovoimakentissä)
• Pallopeilin polttoväli on puolet kaarevuussäteestä.
• Kupera pallopeili hajoittaa säteet ja f < 0.
• Kovera kokoo säteet ja f > 0.
• Kuvan paikka voidaan hahmotella piirtämällä kappaleen pohja optiselle akselille ja kappaleen pää paikkaan, jossa valonsäteet leikkaavat. Valonsäteet voidaan piirtää käyttäen kolmea sääntöä:

1. Optisen akselin kautta kulkevat valonsäteet (tai niiden jatkeet) kulkevat aina polttopisteen kautta.
2. Peilin keskipisteeseen osuvan säteen tulo ja heijastuskulma ovat samat.
3. Säde (tai säteen jatke), joka kulkee kaarevuuskeskipisteen kautta heijastuu suoraan takaisin.

• Kuperan linssin polttoväli f > 0.
• Koveran linssin polttoväli f < 0.
• Sekä peilillä että linssillä kuva on valekuva, jos kaikki valonsäteet eivät kulje kuvan kärjen kautta, vaan vähintään osa säteistä on säteiden jatkeita.
• Kuvausyhtälö toimii niin peilille kuin linssille:[[$ { 1 \over a } + { 1 \over b } = { 1 \over f } $]]​.
• a on esineen etäisyys linssistä, b on kuvan etäisyys linssistä (b < 0, jos valekuva) ja f on linssin polttoväli.
• Viivasuurennus toimii niin peilille kuin linssille: [[$ m = { k \over e } = { |b| \over |a|} $]]​.
• k on kuvan korkeus, e on esineen korkeus ja a ja b kuten yllä.
• Linssisysteemeissä ensimmäisestä linssistä syntyvää kuvaa käytetään seuraavan linssin esineenä. Ensimmäisestä linssistä syntyvää kuvaa käytetään seuraavalle linssille vale-esineenä, eli a < 0 jos kuva syntyy toisen linssin taakse eikä eteen.