KE3S
Kpl.3.2
3.8







3.10
_2%5Cright)%3D30kg%3D30%5Ccdot10%5E3g)
_2%5Cright)%3D60%7B%2C%7D062%5C%20%5Cfrac%7Bg%7D%7Bmol%7D)

%3D%3F)
_2%5Cright)%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B30%5Ccdot10%5E3%5C%20g%7D%7B60%7B%2C%7D062%5C%20%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D499%7B%2C%7D5%5C%20mol)
%7D%7Bn%5Cleft(CO%5Cleft(NH_2%5Cright)_2%5Cright)%7D%3D%5Cfrac%7B2%7D%7B1%7D) , joten
, joten
%3D2%5Ccdot499%7B%2C%7D5%5C%20mol%3D999%7B%2C%7D0%5C%20mol)
%3DnV_m%3D999%7B%2C%7D0%5C%20mol%5Ccdot22%7B%2C%7D41%5C%20%5Cfrac%7Bdm%5E3%7D%7Bmol%7D%3D22%5C%20390%5C%20dm%5E3%5Capprox22%5C%20000%5C%20dm%5E3%3D22%5C%20m%5E3)
3.12
%3D1%7B%2C%7D00g)
%3D0%7B%2C%7D934%5C%20l%3D0%7B%2C%7D934%5C%20dm%5E3)


%2B2HCl%5Cleft(aq%5Cright)%5Crightarrow%20xCl_2%5Cleft(aq%5Cright)%2BH_2%5Cleft(g%5Cright))
%3D%5Cfrac%7BV%5Cleft(H_2%5Cright)%7D%7BV_m%7D%3D%5Cfrac%7B0%7B%2C%7D934%5C%20dm%5E3%7D%7B22%7B%2C%7D41%5C%20%5Cfrac%7Bdm%5E3%7D%7Bmol%7D%7D%3D0%7B%2C%7D41678%5C%20mol)
%7D%7Bn%5Cleft(H_2%5Cright)%7D%3D%5Cfrac%7B1%7D%7B1%7D%5C%20%5CLeftrightarrow%5C%20n%5Cleft(x%5Cright)%3D1%5Ccdot0%7B%2C%7D41678%5C%20mol)
 , josta
, josta
%3D%5Cfrac%7Bm%7D%7Bn%7D%3D%5Cfrac%7B1%7B%2C%7D00%5C%20g%7D%7B0%7B%2C%7D041678%5C%20mol%7D%3D23%7B%2C%7D993%5C%20%5Cfrac%7Bg%7D%7Bmol%7D)
3.13
a)
%2B2Na%5Cleft(l%5Cright))
b)


%3D120g)
%3D65%7B%2C%7D02%5C%20%5Cfrac%7Bg%7D%7Bmol%7D)

%3D%3F)
%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B120g%7D%7B65%7B%2C%7D02%5C%20%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D1%7B%2C%7D8456%5C%20mol)
%7D%7Bn%5Cleft(NaN_3%5Cright)%7D%3D%5Cfrac%7B3%7D%7B2%7D%5Crightarrow%20n%5Cleft(N_2%5Cright)%3D%5Cfrac%7B3%7D%7B2%7D%5Ccdot%20n%5Cleft(NaN_3%5Cright)%3D%5Cfrac%7B3%7D%7B2%7D%5Ccdot1%7B%2C%7D8456%5C%20mol%3D2%7B%2C%7D7684%5C%20mol)

%3D%5Cfrac%7B2%7B%2C%7D7684%5C%20mol%5Ccdot8%7B%2C%7D31451%5C%20%5Cfrac%7BPa%5Ccdot%20m%5E3%7D%7Bmol%5Ccdot%5C%20K%7D%5Ccdot313%7B%2C%7D15K%7D%7B120%5Ccdot10%5E3Pa%7D%3D0%7B%2C%7D060067%5C%20m%5E3%5Capprox60%7B%2C%7D1%5C%20dm%5E3)
3.15
3.10
3.12
Kaavasta  voidaan päätellä, että kysytty metalli muodostaaa ionin
voidaan päätellä, että kysytty metalli muodostaaa ionin  , joten se voisi olla jokin toisen pääryhmän metalleista, Taulukkokirjan mukaan M(Mg)=24,31 g/mol, joten se on lähimpänä ratkaisua moolimasassaa. Mettalli oli siis magnesiumia.
, joten se voisi olla jokin toisen pääryhmän metalleista, Taulukkokirjan mukaan M(Mg)=24,31 g/mol, joten se on lähimpänä ratkaisua moolimasassaa. Mettalli oli siis magnesiumia.
3.13
a)
b)
c)
Typpi kaasun tilavuus olisi suurempi, sillä normaali paine on pienempi (noin 101 kPa) kui 120 kPa. Kun paine pienenee, kaasun tilavuus kasvaa vakiolämpötilassa.
3.15
Kpl.5.2
5.12
a ja c
5.13
a)

%3D-847%7B%2C%7D8kJ)
b)


c)

%5Cright)%3D-176%7B%2C%7D5kJ%5Capprox177kJ)
d)
a ja c
5.13
a)
b)
c)
d)
Kpl. 4.4
4.21
a)
4.23
4.24
4.27
a)
4.23
4.24
4.27
Kpl. 4.3
Kpl. 4.2
Kpl.4.1
4.1
a) Hapettuminen
b) Pelkistyminen
c) Pelkistyminen
d) Pelkistyminen
e) Hapettuminen
4.2
A-4 Pelkistyminen
B-1 Hapettuminen
C-2 Hapettuminen
D-3 Pelkistyminen
4.3
a)

Metanaali ja metaanihappo
b)

1-Propanoli
c)
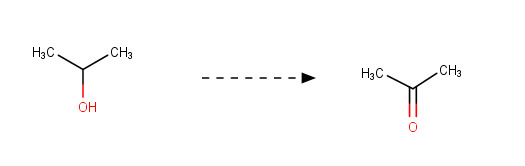
2-Probanoni
d)
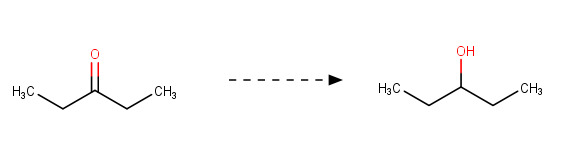
3-pentanoli
e)

Butanaali ja 1-butanoli
4.4
a)

b)

c)
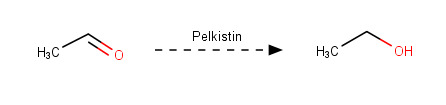
d)

4.5

A: 2-metyylibutanaali
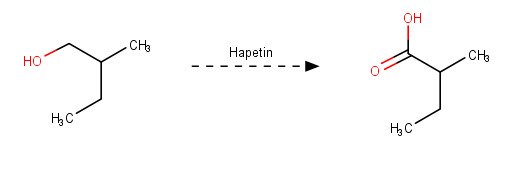
B: 2-metyyli-1-butanoli
C: 2-metyylibutaanihappo

Yhdisteen D muodostumisreaktio on neutraloitumisreaktio
4.6
m-%(C) = 68,4 %
m-%(H) = 11,4 %
m-%(O) = 20,2 %
Ratkaistaan ensin yhdisteen X suhde- eli empiirinen kaava olettaen, että yhdistettä on 100 grammaa.
Tämä massa sisältää massaprosenttisen koostumuksen perusteella eri alkuaineita seuraavasti:
m(C) = 68,4 g
m(H) = 11,4 g
m(O) = 20,2 g
Ratkaistaan alkuaineatomien ainemäärä:
%3D%5Cfrac%7Bm%5Cleft(C%5Cright)%7D%7BM%5Cleft(C%5Cright)%7D%3D%5Cfrac%7B68%7B%2C%7D4g%7D%7B12%7B%2C%7D01%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D5%7B%2C%7D6953mol)
%3D%5Cfrac%7Bm%5Cleft(H%5Cright)%7D%7BM%5Cleft(H%5Cright)%7D%3D%5Cfrac%7B11%7B%2C%7D4g%7D%7B1%7B%2C%7D008%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D11%7B%2C%7D310mol)
%3D%5Cfrac%7Bm%5Cleft(O%5Cright)%7D%7BM%5Cleft(O%5Cright)%7D%3D%5Cfrac%7B20%7B%2C%7D2g%7D%7B16%7B%2C%7D00%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D1%7B%2C%7D2625mol)
Jaetaan kukin ainemäärä pienimmällä (hapen) ainemäärällä, jolloin ainemäärien suhteeksi saadaan
n(C) : n(H) : n(O) = 4,50 : 8,96: 1.
Tästä saadaan pienimpien kokonaislukujen suhteeksi 9:18:2 kertomalla kukin luku kahdella.
Yhdisteen X suhdekaava on siten (C9H18O2)x.
Lasketaan x:n arvo lausekkeesta x ∙ (9 ∙ 12,01 + 18 ∙ 1,008 + 2 ∙ 16,00) = 158, josta 158,23 x = 158 => x = 1.
Yhdisteen X molekyylikaava on siten C9H18O2.
Koska yhdisteessä on kaksi happiatomia, kyseessä voi olla karboksyylihappo tai esteri. Tiedetään, että yhdiste pelkistyy, jolloin syntyy yhdistettä Y, jossa IR-tutkimuksen mukaan on alkoholeille tyypillinen hydroksyyliryhmä. Eli pelkistymisreaktiossa on muodostunut alkoholia. X:n tulee siten olla karboksyylihappo, joka pelkistyy primääriseksi alkoholiksi.
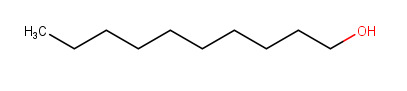
Yhdisteen X rakennekaava on

Yhdisteen Y rakennekaava on
a) Hapettuminen
b) Pelkistyminen
c) Pelkistyminen
d) Pelkistyminen
e) Hapettuminen
4.2
A-4 Pelkistyminen
B-1 Hapettuminen
C-2 Hapettuminen
D-3 Pelkistyminen
4.3
a)

Metanaali ja metaanihappo
b)

1-Propanoli
c)

2-Probanoni
d)

3-pentanoli
e)

Butanaali ja 1-butanoli
4.4
a)

b)

c)

d)

4.5

A: 2-metyylibutanaali

B: 2-metyyli-1-butanoli
C: 2-metyylibutaanihappo

Yhdisteen D muodostumisreaktio on neutraloitumisreaktio
4.6
m-%(C) = 68,4 %
m-%(H) = 11,4 %
m-%(O) = 20,2 %
Ratkaistaan ensin yhdisteen X suhde- eli empiirinen kaava olettaen, että yhdistettä on 100 grammaa.
Tämä massa sisältää massaprosenttisen koostumuksen perusteella eri alkuaineita seuraavasti:
m(C) = 68,4 g
m(H) = 11,4 g
m(O) = 20,2 g
Ratkaistaan alkuaineatomien ainemäärä:
Jaetaan kukin ainemäärä pienimmällä (hapen) ainemäärällä, jolloin ainemäärien suhteeksi saadaan
n(C) : n(H) : n(O) = 4,50 : 8,96: 1.
Tästä saadaan pienimpien kokonaislukujen suhteeksi 9:18:2 kertomalla kukin luku kahdella.
Yhdisteen X suhdekaava on siten (C9H18O2)x.
Lasketaan x:n arvo lausekkeesta x ∙ (9 ∙ 12,01 + 18 ∙ 1,008 + 2 ∙ 16,00) = 158, josta 158,23 x = 158 => x = 1.
Yhdisteen X molekyylikaava on siten C9H18O2.
Koska yhdisteessä on kaksi happiatomia, kyseessä voi olla karboksyylihappo tai esteri. Tiedetään, että yhdiste pelkistyy, jolloin syntyy yhdistettä Y, jossa IR-tutkimuksen mukaan on alkoholeille tyypillinen hydroksyyliryhmä. Eli pelkistymisreaktiossa on muodostunut alkoholia. X:n tulee siten olla karboksyylihappo, joka pelkistyy primääriseksi alkoholiksi.
Yhdisteen X rakennekaava on

Yhdisteen Y rakennekaava on

Kpl.3.1
3.1

3.2
a)
Rikkihappo
b)
n(O2)=1,5mol
2,0 mol-1,5 mol=0,5 mol
c)
3 mol
3.5
%3D1%7B%2C%7D93%5C%20g)
%3D26%7B%2C%7D036%5C%20%5Cfrac%7Bg%7D%7Bmol%7D)
%3D3%7B%2C%7D45%5C%20g)
%3D32%7B%2C%7D00%5C%20%5Cfrac%7Bg%7D%7Bmol%7D)
%3D%3F)
%2B5O_2%5Cleft(g%5Cright)%5Crightarrow4CO_2%5Cleft(g%5Cright)%2B2H_2O%5Cleft(g%5Cright))
%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B1%7B%2C%7D93%5C%20g%7D%7B26%7B%2C%7D036%5C%20%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D0%7B%2C%7D074128%5C%20mol)
%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B3%7B%2C%7D45%5C%20g%7D%7B32%7B%2C%7D00%5C%20%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D0%7B%2C%7D10781%5C%20mol)
%7D%7Bn%5Cleft(C_2H_2%5Cright)%7D%3D%5Cfrac%7B5%7D%7B2%7D)
%3D%5Cfrac%7B5%7D%7B2%7D%5Ccdot0%7B%2C%7D074128%5C%20mol%3D0%7B%2C%7D18532%5C%20mol)
%3DnM%3D0%7B%2C%7D18532%5C%20mol%5Ccdot32%7B%2C%7D00%5C%20%5Cfrac%7Bg%7D%7Bmol%7D%3D5%7B%2C%7D9302g%5Capprox5%7B%2C%7D93g)

3.2
a)
Rikkihappo
b)
n(O2)=1,5mol
2,0 mol-1,5 mol=0,5 mol
c)
3 mol
3.5
Koska happea tarvitaan 0,18532 moolia, ja tässä on saatavilla vain 0,10781 moolia, happi on tällöin rajoittava tekijä. Palaminen ei siten ole täydellistä.
Ratkaistaan täydelliseen palamiseen tarvittava hapen massa täydelliseen palamiseen tarvittavan hapen ainemäärän avulla:
Kpl.2.4
2.18
a)
%5Crightarrow%20MgO%5Cleft(g%5Cright)%2BCO_2%5Cleft(g%5Cright))
%5Crightarrow2H_2O%5Cleft(l%5Cright)%2BO_2%5Cleft(g%5Cright))
d)
%5Crightarrow%20N_2O%5Cleft(g%5Cright)%2B2H_2O%5Cleft(g%5Cright))
%5Crightarrow2N_2%5Cleft(g%5Cright)%2BO_2%5Cleft(g%5Cright))
e)
%5Crightarrow%20O_2%5Cleft(g%5Cright)%2BO%5Cleft(g%5Cright))
f)
%5Crightarrow2Ag%5Cleft(s%5Cright)%2BF_2%5Cleft(g%5Cright))
2.19
a)
%2B2Na%5Cleft(l%5Cright)) b)
b)
%3D40l)
%3D1%7B%2C%7D20%5C%20%5Cfrac%7Bg%7D%7Bl%7D)
%3D1%7B%2C%7D20g%5Ccdot40l%3D48g)
%3D%3F)
%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B48%7B%2C%7D00%5C%20g%7D%7B28%7B%2C%7D02%5C%20%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D1%7B%2C%7D713%5C%20mol)
%7D%7Bn%5Cleft(N_3%5Cright)%7D%3D%5Cfrac%7B2%7D%7B3%7D) ,joten
,joten
%3D%5Cfrac%7B2%7D%7B3%7D%5Ccdot1%7B%2C%7D713mol%3D1%7B%2C%7D142%5C%20mol)
%3DnM%5Ccdot1%7B%2C%7D142%5C%20mol%5Ccdot65%7B%2C%7D02%5C%20%5Cfrac%7Bg%7D%7Bmol%7D%3D74%7B%2C%7D25%5Capprox74%5C%20g)
2.22
%3D1%7B%2C%7D56%5C%20mol)
%3D152%7B%2C%7D072%5C%20%5Cfrac%7Bg%7D%7Bmol%7D)
%3D18%7B%2C%7D016%5C%20%5Cfrac%7Bg%7D%7Bmol%7D)
%3D%3F)
%3D%3F)
%2B2H_2O%5Cleft(g%5Cright)%2BN_2%5Cleft(g%5Cright))
%7D%7Bn%5Cleft(kaasut%5Cright)%7D%3D%5Cfrac%7B1%7D%7B5%7D) , joten
, joten
%3D%5Cfrac%7B1%7D%7B5%7D%5Ccdot1%7B%2C%7D56%5C%20mol%3D0%7B%2C%7D312%5C%20mol)
%3DnM%3D0%7B%2C%7D312%5C%20mol%5Ccdot152%7B%2C%7D072%5C%20%5Cfrac%7Bg%7D%7Bmol%7D%3D47%7B%2C%7D446464%5Capprox47%7B%2C%7D4%5C%20g)
%7D%7Bn%5Cleft(C_2H_4N_2O_6%5Cright)%7D%3D%5Cfrac%7B2%7D%7B1%7D) , joten
, joten
%3D2%5Ccdot0%7B%2C%7D312%5C%20mol%3D0%7B%2C%7D624%5C%20mol)
%3DnM%3D0%7B%2C%7D624%5C%20mol%5Ccdot18%7B%2C%7D016%5C%20%5Cfrac%7Bg%7D%7Bmol%7D%3D11%7B%2C%7D241984...%5Capprox11%7B%2C%7D2g)
a)
b)
%5Crightarrow2KCl%5Cleft(g%5Cright)%2B3O_2%5Cleft(g%5Cright))
c)d)
e)
f)
2.19
a)
2.22
Kpl.2.3
2.13
b, c, e
2.14
a)
ei
b)
Kyllä,

c)
Kyllä,

2-17
b, c, e
2.14
a)
ei
b)
Kyllä,
c)
Kyllä,
2-17
Kpl.2.2
2.8
a)
%2BH_2O%5Cleft(l%5Cright)%5Crightarrow%20H_3O%5E%2B%5Cleft(aq%5Cright)%2BNO_3%5E-%5Cleft(aq%5Cright)) pH<7
b)
pH<7
b)
%2BH_2O%5Cleft(l%5Cright)%5Crightarrow%20H_2O%5E%2B%5Cleft(l%5Cright)%2BOH%5E-%5Cleft(aq%5Cright)) pH>7
pH>7
2.9
a)
%2BCH_3COOH%5Cleft(aq%5Cright)%5Crightarrow%20NH_4CH_3COO%5Cleft(aq%5Cright))
%2BCH_3COOH%5Cleft(aq%5Cright)%5Crightarrow%20NH_4CH_3COO%5Cleft(aq%5Cright)%2BH_2O%5Cleft(l%5Cright))
a)
%3D0%7B%2C%7D15%5C%20%5Cfrac%7Bmol%7D%7Bdm%5E3%7D)
%3D10ml%3D0%7B%2C%7D010dm%5E3)
%3D0%7B%2C%7D035%5C%20%5Cfrac%7Bmol%7D%7Bdm%5E3%7D)
%3D%3F)

%3DcV%3D0%7B%2C%7D15%5C%20%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%5Ccdot0%7B%2C%7D010dm%5E3%3D0%7B%2C%7D0015%5C%20mol)
%7D%7Bn%5Cleft(H_2SO_4%5Cright)%7D%3D%5Cfrac%7B2%7D%7B1%7D) , joten
, joten
%3D2%5Ccdot0%7B%2C%7D0015%5C%20mol%3D0%7B%2C%7D003%5C%20mol)
%3D%5Cfrac%7Bn%7D%7Bc%7D%3D%5Cfrac%7B0%7B%2C%7D003mol%7D%7B0%7B%2C%7D035%5C%20%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%7D%3D0%7B%2C%7D08571...dm%5E3%5C%20%5Capprox86ml)
b)
%3D1%7B%2C%7D65g)
%3D36%7B%2C%7D458%5Cfrac%7Bg%7D%7Bmol%7D)
%3D1%7B%2C%7D0%5C%20l%3D1%7B%2C%7D0dm%5E3)
%3D40ml%3D0%7B%2C%7D040dm%5E3)
_2%5Cright)%3D0%7B%2C%7D025%5C%20%5Cfrac%7Bmol%7D%7Bdm%5E3%7D)
_2%5Cright)%3D%3F)
_2%5Cleft(aq%5Cright)%2B2HCl%5Cleft(aq%5Cright)%5Crightarrow%20Ca%5Cleft(Cl%5Cright)_2%5Cleft(aq%5Cright)%2B2H_2O%5Cleft(l%5Cright))
%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B1%7B%2C%7D65%5C%20g%7D%7B36%7B%2C%7D458%5C%20%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D0%7B%2C%7D045258%5C%20mol)
%3D%5Cfrac%7Bn%7D%7BV_1%7D%3D%5Cfrac%7B0%7B%2C%7D045258%5C%20mol%7D%7B1%7B%2C%7D0%5C%20dm%5E3%7D%3D0%7B%2C%7D045258%5C%20%5Cfrac%7Bmol%7D%7Bdm%5E3%7D)
%3DcV_2%3D0%7B%2C%7D045258%5C%20%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%5Ccdot0%7B%2C%7D040%5C%20dm%5E3%3D0%7B%2C%7D001812%5C%20mol)
_2%5Cright)%7D%7Bn%5Cleft(HCl%5Cright)%7D%3D%5Cfrac%7B1%7D%7B2%7D) , joten
, joten _2%5Cright)%3D%5Cfrac%7B1%7D%7B2%7D%5Ccdot0%7B%2C%7D001812%5C%20mol%3D0%7B%2C%7D0009060%5C%20mol)
_2%5Cright)%3D%5Cfrac%7Bn%7D%7Bc%7D%3D%5Cfrac%7B0%7B%2C%7D0009060%5C%20mol%7D%7B0%7B%2C%7D025%5C%20%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%7D%3D0%7B%2C%7D03624%5C%20dm%5E3%3D36%5C%20ml)
c)
_2%5Cright)%3D130%5C%20mg%3D0%7B%2C%7D130g)
_2%5Cright)%3D58%7B%2C%7D326%5C%20%5Cfrac%7Bg%7D%7Bmol%7D)
%3D0%7B%2C%7D075%5C%20%5Cfrac%7Bmol%7D%7Bdm%5E3%7D)
%3D%3F)
%2B3Mg%5Cleft(OH%5Cright)_2%5Cleft(aq%5Cright)%5Crightarrow%20Mg_3%5Cleft(PO_4%5Cright)_2%5Cleft(aq%5Cright)%2B3H_2O%5Cleft(l%5Cright))
_2%5Cright)%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B0%7B%2C%7D130%5C%20g%7D%7B58%7B%2C%7D326%5C%20%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D0%7B%2C%7D0022289%5C%20mol)
%7D%7Bn%5Cleft(Mg%5Cleft(OH%5Cright)_2%5Cright)%7D%3D%5Cfrac%7B2%7D%7B3%7D) , joten
, joten %3D%5Cfrac%7B2%7D%7B3%7D%5Ccdot0%7B%2C%7D0022289%5C%20mol%3D0%7B%2C%7D0014859%5C%20mol)
%3D%5Cfrac%7Bn%7D%7Bc%7D%3D%5Cfrac%7B0%7B%2C%7D0014859%5C%20mol%7D%7B0%7B%2C%7D075%5C%20%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%7D%3D0%7B%2C%7D01981...dm%5E3%5Capprox20ml)
2.11
%3D25%7B%2C%7D37%5C%20g)
%3D250%5C%20cm%5E3%3D250%5C%20ml)
%3D10%7B%2C%7D0%5C%20ml)
%3D0%7B%2C%7D036%5C%20%5Cfrac%7Bmol%7D%7Bdm%5E3%7D)
%3D37%7B%2C%7D3%5C%20ml%3D0%7B%2C%7D0373dm%5E3)
%3D17%7B%2C%7D034%5C%20%5Cfrac%7Bg%7D%7Bmol%7D)
%3D%3F)
%2BH_2SO_4%5Cleft(aq%5Cright)%5Crightarrow%5Cleft(NH_4%5Cright)_2SO_4%5Cleft(aq%5Cright))
%3DcV%3D0%7B%2C%7D036%5C%20%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%5Ccdot0%7B%2C%7D0373%5C%20dm%5E3%3D0%7B%2C%7D001343mol)
%7D%7Bn%5Cleft(H_2SO_4%5Cright)%7D%3D%5Cfrac%7B2%7D%7B1%7D) , joten
, joten %3D2%5Ccdot0%7B%2C%7D001343%5C%20mol%3D0%7B%2C%7D002686%5C%20mol)
%3DnM%3D0%7B%2C%7D002686%5C%20mol%5Ccdot17%7B%2C%7D034%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%3D0%7B%2C%7D04575g)

%3D%5Cfrac%7Bm%5Cleft(NH_3%5Cright)%7D%7Bm%5Cleft(N%C3%A4yte%5Cright)%7D%5Ccdot100%5C%25%3D%5Cfrac%7B1%7B%2C%7D144g%7D%7B23%7B%2C%7D37g%7D%3D4%7B%2C%7D509%5C%25%5Capprox4%7B%2C%7D5%5C%25)
a)
c)
%2BH_2O%5Cleft(l%5Cright)%5Crightarrow%20H_3O%5E%2B%5Cleft(aq%5Cright)%2BCH_3COO%5E-%5Cleft(aq%5Cright)) pH<7
pH<7
d)
%2BH_2O%5Cleft(l%5Cright)%5Crightarrow%20CH_3COOH%5Cleft(aq%5Cright)%2BOH%5E-%5Cleft(aq%5Cright)) pH>7
pH>7
e)
%2B2H_2O%5Cleft(l%5Cright)%5Crightarrow2H_3O%5E%2B%5Cleft(aq%5Cright)%2BSO_4%5E%7B2-%7D%5Cleft(aq%5Cright)) pH<7
pH<7
f)
%2BH_2O%5Cleft(l%5Cright)%5Crightarrow%20CH_3NH_3%5E%2B%5Cleft(aq%5Cright)%2BOH%5E-%5Cleft(aq%5Cright)) pH>7
pH>7
2.9
a)
Ammoniumasetaatti eli ammoniumetanaatti
n(emäs)=2,0mol
b)
_3%5Cleft(aq%5Cright)%2B3H_2SO_4%5Cleft(aq%5Cright)%5Crightarrow2Al%5Cleft(SO_4%5Cright)_3%2B6H_2O)
Alumiinisulfaatti
n(emäs)=1,3mol
c)
%2B3KOH%5Cleft(aq%5Cright)%5Crightarrow%2BK_3PO_4%5Cleft(aq%5Cright)%2B3H_2O%5Cleft(l%5Cright))
kaliumfosfaatti
n(emäs)=2mol
2.10d)
%2BCa%5Cleft(OH%5Cright)_2%5Crightarrow%20Ca%5Cleft(CH_3CH_2COO%5Cright)%5Cleft(aq%5Cright)%2B2H_2O%5Cleft(l%5Cright))
Kalsiumpropanaatti
n(emäs)=1,0mol
a)
b)
c)
Ammoniakin massa titratussa näytteessä (10,0 ml):
Puhdistuainetta oli 250 ml, joten ammoniakkia olisi
Kpl.2.1
2.1
Happetumis- ja pelkistymis reaktioon
2.2
2.3
a) Oikein, Väärin, Oikein
b) Väärin, Väärin, Väärin
c) Oikein, Oikein, Oikein
2.5
a)
%2BS%5Cleft(s%5Cright)%5Crightarrow%20Ag_2S%5Cleft(s%5Cright)) Hapetin: S
Hapetin: S
%2B2Br%5E-%5Cleft(aq%5Cright)%5Crightarrow2Cl%5E-%5Cleft(aq%5Cright)%2BBr_2%5Cleft(aq%5Cright)) Hapetin:
Hapetin:
e)
%2BCu%5E%7B2%2B%7D%5Cleft(aq%5Cright)%5Crightarrow%20Fe%5E%7B2%2B%7D%2B%5Cleft(aq%5Cright)%2BCu%5Cleft(s%5Cright)) Hapetin:
Hapetin: 
2.6
a)
Alumiini hapettuu, rauta(III)-ionit pelkistyvät
b)
Alumini pelkistin, rauta(III) hapetin
c)
%3D100g)
%3D55%7B%2C%7D85%5Cfrac%7Bg%7D%7Bmol%7D)
%3D26%7B%2C%7D98%5Cfrac%7Bg%7D%7Bmol%7D)
%3D159%7B%2C%7D70%5Cfrac%7Bg%7D%7Bmol%7D)
%3D%3F)
%3D%3F)
%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B100g%7D%7B55%7B%2C%7D85%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D1%7B%2C%7D79051mol)
%7D%7Bn%5Cleft(Fe%5Cright)%7D%3D%5Cfrac%7B2%7D%7B2%7D) , joten
, joten
%3Dn%5Cleft(Fe%5Cright)%3D1%7B%2C%7D79051mol)
%7D%7Bn%5Cleft(Fe%5Cright)%7D%3D%5Cfrac%7B1%7D%7B2%7D) ,joten
,joten %3D%5Cfrac%7B1%7D%7B2%7D%5Ccdot%20n%5Cleft(Fe%5Cright)%3D1%7B%2C%7D79051mol%5Ccdot%5Cfrac%7B1%7D%7B2%7D%3D0%7B%2C%7D895255mol)
%3D1%7B%2C%7D79051mol%5Ccdot26%7B%2C%7D98%5Cfrac%7Bg%7D%7Bmol%7D%3D48%7B%2C%7D307...%5Capprox48%7B%2C%7D31g)
%3D0%7B%2C%7D895255mol%5Ccdot159%7B%2C%7D70%5Cfrac%7Bg%7D%7Bmol%7D%3D142%7B%2C%7D972...%5Capprox143%7B%2C%7D0g)
Happetumis- ja pelkistymis reaktioon
2.2
| Reaktio | Muodostuvan ionin kaava | Hapetusluku |
| Natriumatomi hapettuu | Na+ | +I |
| Jodiatomi pelkistyy | I- | -I |
| Rikkiatomi pelkiistyy | S2- | -II |
| Magnestiumatomi hapettuu | Mg2+ | +II |
| Rauta(II)-ioni hapettuu | Fe3+ | +III |
| Nikkeli(III)-ioni pelkistyy | Ni2+ | +II |
| Tina(II)-ioni hapettuu | Sn4+ | +IV |
| Fosforiatomi pelkistyy | P3- | -III |
2.3
a) Oikein, Väärin, Oikein
b) Väärin, Väärin, Väärin
c) Oikein, Oikein, Oikein
2.5
a)
b)
%2BN_2%5Cleft(g%5Cright)%5Crightarrow2Na_3N%5Cleft(s%5Cright)) Hapetin:
Hapetin: 
c)
%2B3Cl_2%5Cleft(g%5Cright)%5Crightarrow2AlCl_3%5Cleft(l%5Cright)) Hapetin:
Hapetin:
d)e)
2.6
a)
Alumiini hapettuu, rauta(III)-ionit pelkistyvät
b)
Alumini pelkistin, rauta(III) hapetin
c)
Ratkaistaan syntyvän raudan ainemäärä:
Tasapainotetun reaktioyhtälön perusteella:
Tasapainotetun reaktioyhtälön perusteella:
Testaa oppimasi
1) c, d
2) a
3) a, b, c
4) b
5) a, b, c
6) d
7) d
8) a, b
9) b
10) d
Käsitetesti
Aktivoitumisenergia - On siirtymäkompleksin mudostumiseen tarvittava energiamäärä
Eksoterminen reaktio - On reaktio, jossa vapautuu lämpöenergiaa
Entalpia - On suure, joka kuvaa aieeseen varastoitunutta kemiallista energiaa
Prosentuaalinen saanto - Kuvaa, kuinka monta prosenttia reaktiotuotteena asaadun aineen määrä on teoreettisesta määrästä
Reaktiotuote - On aine, joka muodostuu kemiallisessa reaktiossa
Siirtymäkompleksi - On runsasenerginen, lyhytkäinen reaktion välituote
Sponstaani reaktio - On reaktio, joka taoatuu tietyissä olosuhteissa ilan ulkoista pakotetta
Teoreettinen saanto - On tasapainotetun reaktioyhtälön kertoimien mukaan laskettu reaktiotuotteiden enimmäismäärä
2) a
3) a, b, c
4) b
5) a, b, c
6) d
7) d
8) a, b
9) b
10) d
Käsitetesti
Aktivoitumisenergia - On siirtymäkompleksin mudostumiseen tarvittava energiamäärä
Eksoterminen reaktio - On reaktio, jossa vapautuu lämpöenergiaa
Entalpia - On suure, joka kuvaa aieeseen varastoitunutta kemiallista energiaa
Prosentuaalinen saanto - Kuvaa, kuinka monta prosenttia reaktiotuotteena asaadun aineen määrä on teoreettisesta määrästä
Reaktiotuote - On aine, joka muodostuu kemiallisessa reaktiossa
Siirtymäkompleksi - On runsasenerginen, lyhytkäinen reaktion välituote
Sponstaani reaktio - On reaktio, joka taoatuu tietyissä olosuhteissa ilan ulkoista pakotetta
Teoreettinen saanto - On tasapainotetun reaktioyhtälön kertoimien mukaan laskettu reaktiotuotteiden enimmäismäärä
Kpl.1.3
1.12
a) Oikein
b) Väärin, 0,67 mol
c) Oikein
d) Väärin, 4,0 mol
e) Oikein
f) Oikein
1.13
a)
%2BO_2%5Cleft(g%5Cright)%5Crightarrow2H_2O%5Cleft(l%5Cright))
%3D10%7B%2C%7D0g)
%3D1%7B%2C%7D008%5Cfrac%7Bg%7D%7Bmol%7D%5Ccdot2%3D2%7B%2C%7D016%5Cfrac%7Bg%7D%7Bmol%7D)
%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B10%7B%2C%7D0g%7D%7B2%7B%2C%7D016%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D4%7B%2C%7D96031...%5Capprox4%7B%2C%7D9603mol)
%7D%7Bn%5Cleft(H_2%5Cright)%7D%3D%5Cfrac%7B1%7D%7B2%7D)
%3D%5Cfrac%7B1%7D%7B2%7D%5Ccdot%20n%5Cleft(H_2%5Cright)%3D%5Cfrac%7B1%7D%7B2%7D%5Ccdot4%7B%2C%7D9603%5Cfrac%7Bg%7D%7Bmol%7D%3D2%7B%2C%7D048015mol)
%3D16%7B%2C%7D00%5Cfrac%7Bg%7D%7Bmol%7D%5Ccdot2%3D32%7B%2C%7D00%5Cfrac%7Bg%7D%7Bmol%7D)
%3Dn%5Ccdot%20M%3D2%7B%2C%7D048015mol%5Ccdot32%7B%2C%7D00%5Cfrac%7Bg%7D%7Bmol%7D%3D79%7B%2C%7D3648...%5Capprox76%7B%2C%7D4g)
b)
%2BO_2%5Cleft(g%5Cright)%5Crightarrow2H_2O%5Cleft(l%5Cright))
%3D10%7B%2C%7D0g)
%3D1%7B%2C%7D008%5Cfrac%7Bg%7D%7Bmol%7D%5Ccdot2%3D2%7B%2C%7D016%5Cfrac%7Bg%7D%7Bmol%7D)
%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B10%7B%2C%7D0g%7D%7B2%7B%2C%7D016%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D4%7B%2C%7D96031...%5Capprox4%7B%2C%7D9603mol)
%7D%7Bn%5Cleft(H_2%5Cright)%7D%3D%5Cfrac%7B2%7D%7B2%7D)
%3D%5Cfrac%7B2%7D%7B2%7D%5Ccdot%20n%5Cleft(H_2%5Cright)%3D1%5Ccdot4%7B%2C%7D9603%5C%20mol%3D4%7B%2C%7D9603mol)
%3D18%7B%2C%7D01528%5Cfrac%7Bg%7D%7Bmol%7D)
%3Dn%5Ccdot%20M%3D4%7B%2C%7D9603%5Cfrac%7Bg%7D%7Bmol%7D%5Ccdot18%7B%2C%7D01528%5Cfrac%7Bg%7D%7Bmol%7D%3D89%7B%2C%7D3611...%5Capprox89%7B%2C%7D4g%3D0%7B%2C%7D0894kg)
c)
%2BO_2%5Cleft(g%5Cright)%5Crightarrow2H_2O%5Cleft(l%5Cright))
H=4
O=2
1.14
a)
%2BO_2%5Cleft(g%5Cright)%5Crightarrow%20N_2%5Cleft(g%5Cright)%2B2H_2O%5Cleft(g%5Cright))
b)
%2BO_2%5Cleft(g%5Cright)%5Crightarrow%20N_2%5Cleft(g%5Cright)%2B2H_2O%5Cleft(g%5Cright))
%3D150g)
%3D32%7B%2C%7D0452%5Cfrac%7Bg%7D%7Bmol%7D)
%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B150%7B%2C%7D0g%7D%7B32%7B%2C%7D0452%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D4%7B%2C%7D6808...%5Capprox4%7B%2C%7D681mol)
%7D%7Bn%5Cleft(N_2H_4%5Cright)%7D%3D%5Cfrac%7B1%7D%7B1%7D)
%3D%5Cfrac%7B1%7D%7B1%7D%5Ccdot%20n%5Cleft(N_2H_4%5Cright)%3D1%5Ccdot4%7B%2C%7D681mol%3D4%7B%2C%7D681mol)
%3D2%5Ccdot16%7B%2C%7D00%3D32%7B%2C%7D00%5Cfrac%7Bg%7D%7Bmol%7D)
%3Dn%5Ccdot%20M%3D4%7B%2C%7D681mol%5Ccdot32%7B%2C%7D00%5Cfrac%7Bg%7D%7Bmol%7D%3D149%7B%2C%7D792%5Capprox150g)
c)
%2BO_2%5Cleft(g%5Cright)%5Crightarrow%20N_2%5Cleft(g%5Cright)%2B2H_2O%5Cleft(g%5Cright))
%3D3%7B%2C%7D0kg%3D3000g)
%3D32%7B%2C%7D0452%5Cfrac%7Bg%7D%7Bmol%7D)
%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B3000g%7D%7B32%7B%2C%7D0452%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D93%7B%2C%7D6177...%5Capprox93%7B%2C%7D618mol)
%7D%7Bn%5Cleft(N_2H_4%5Cright)%7D%3D%5Cfrac%7B3%7D%7B1%7D)
%3D3%5Ccdot93%7B%2C%7D618mol%3D280%7B%2C%7D853...%5Capprox280mol)
1.15
a)
%2B2H_2O%5Cleft(g%5Cright)%5Crightarrow%20O_2%5Cleft(g%5Cright)%2B4NaOH%5Cleft(aq%5Cright))
%3D0%7B%2C%7D50g)
%3D2%5Ccdot16%7B%2C%7D00%5Cfrac%7Bg%7D%7Bmol%7D%3D32%7B%2C%7D00%5Cfrac%7Bg%7D%7Bmol%7D)
%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B0%7B%2C%7D50g%7D%7B32%7B%2C%7D0452%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D0%7B%2C%7D015625mol)
%7D%7Bn%5Cleft(O_2%5Cright)%7D%3D%5Cfrac%7B2%7D%7B1%7D%3D2)
%3D2%5Ccdot0%7B%2C%7D015625mol%3D0%7B%2C%7D03125mol)
%3D77%7B%2C%7D98%5Cfrac%7Bg%7D%7Bmol%7D)
%3Dn%5Ccdot%20M%3D0%7B%2C%7D03125mol%5Ccdot77%7B%2C%7D98%5Cfrac%7Bg%7D%7Bmol%7D%3D2%7B%2C%7D436875g%5Capprox2%7B%2C%7D4g)
b)
%2B2H_2O%5Cleft(g%5Cright)%5Crightarrow%20O_2%5Cleft(g%5Cright)%2B4NaOH%5Cleft(aq%5Cright))
%3D75ml%3D0%7B%2C%7D075dm%5E3)
%3D2%5Ccdot16%7B%2C%7D00%5Cfrac%7Bg%7D%7Bmol%7D%3D32%7B%2C%7D00%5Cfrac%7Bg%7D%7Bmol%7D)
%3D%5Cfrac%7Bm%7D%7BM%7D%3D%5Cfrac%7B0%7B%2C%7D50g%7D%7B32%7B%2C%7D0452%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D0%7B%2C%7D015625mol)
%7D%7Bn%5Cleft(O_2%5Cright)%7D%3D%5Cfrac%7B4%7D%7B1%7D)
%3Dn%5Cleft(O_2%5Cright)%5Ccdot4%3D0%7B%2C%7D0625mol)

%5Crightarrow3O_2%5Cleft(g%5Cright)%2B2KCl%5Cleft(s%5Cright))
%3D2%7B%2C%7D00g)
%3D11%7B%2C%7D450g)
%3D12%7B%2C%7D170g)
%3D12%7B%2C%7D170g-11%7B%2C%7D450g%3D0%7B%2C%7D72g)
%3D122%7B%2C%7D55%5Cfrac%7Bg%7D%7Bmol%7D)
%3D%5Cfrac%7B2%7B%2C%7D00g%7D%7B122%7B%2C%7D55%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D0%7B%2C%7D01631986944%5Capprox0%7B%2C%7D016320mol)
%7D%7Bn%5Cleft(KClO_3%5Cright)%7D%3D%5Cfrac%7B3%7D%7B2%7D)
%3D%5Cfrac%7B3%7D%7B2%7D%5Ccdot%20n%5Cleft(KClO_3%5Cright)%3D0%7B%2C%7D02448mol)
%3Dn%5Ccdot%20M%3D0%7B%2C%7D02448mol%5Ccdot32%7B%2C%7D00%5Cfrac%7Bg%7D%7Bmol%7D%3D0%7B%2C%7D78336)
%3D%5Cfrac%7B0%7B%2C%7D72g%7D%7B0%7B%2C%7D78336...g%7D%3D0%7B%2C%7D9191...%5Capprox0%7B%2C%7D919%3D91%7B%2C%7D9%5C%25)
1.17
a)
%2BHCl(aq)%5Crightarrow%20NaCl(aq)%2BH_2O(l))
%3D25%7B%2C%7D0ml%3D0%7B%2C%7D025dm%5E3)
%3D0%7B%2C%7D10%5Cfrac%7Bmol%7D%7Bdm%5E3%7D)
%3D15%7B%2C%7D8ml%3D0%7B%2C%7D0158dm%5E3)
%3D%3F)
%3DcV%3D0%7B%2C%7D10%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%5Ccdot0%7B%2C%7D0158dm%5E3%3D0%7B%2C%7D00158mol)
%7D%7Bn%5Cleft(NaOH%5Cright)%7D%3D%5Cfrac%7B1%7D%7B1%7D%3D1)
%3D0%7B%2C%7D00158mol%5Ccdot1%3D0%7B%2C%7D00158mol)
%3D%5Cfrac%7Bn%7D%7BV%7D%3D%5Cfrac%7B0%7B%2C%7D00158mol%7D%7B0%7B%2C%7D025dm%5E3%7D%3D0%7B%2C%7D0632%5Cfrac%7Bmol%7D%7Bdm%5E3%7D)
b)
_2(aq)%2B2HNO_3(aq)%5Crightarrow%20Ba%5Cleft(NO_3%5Cright)_2(aq)%2B2H_2O(l))
_2%5Cright)%3D10%7B%2C%7D0ml%3D0%7B%2C%7D010dm%5E3)
_2%5Cright)%3D0%7B%2C%7D00250%5Cfrac%7Bmol%7D%7Bdm%5E3%7D)
%3D0%7B%2C%7D500%5Cfrac%7Bmol%7D%7Bdm%5E3%7D)
%3D%3F)
_2%5Cright)%3DcV%3D0%7B%2C%7D00250%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%5Ccdot0%7B%2C%7D010dm%5E3%3D0%7B%2C%7D000025mol)
%7D%7Bn%5Cleft(Ba%5Cleft(OH%5Cright)_2%5Cright)%7D%3D%5Cfrac%7B2%7D%7B1%7D%3D2)
%3D0%7B%2C%7D000025mol%5Ccdot2%3D0%7B%2C%7D00005mol)
%3D%5Cfrac%7Bn%7D%7Bc%7D%3D%5Cfrac%7B0%7B%2C%7D00005mol%7D%7B0%7B%2C%7D500%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%7D%3D0%7B%2C%7D0001dm%5E3%3D0%7B%2C%7D100ml)
a) Oikein
b) Väärin, 0,67 mol
c) Oikein
d) Väärin, 4,0 mol
e) Oikein
f) Oikein
1.13
a)
b)
c)
H=4
O=2
1.14
a)
b)
c)
1.15
a)
b)
1.16
1.17
a)
b)
Kpl.1.2
1.7
%2B2HCl%5Cleft(aq%5Cright)-%3EZnCl_2%5Cleft(aq%5Cright)%2BH_2%5Cleft(g%5Cright))
-%3E2KCl%5Cleft(s%5Cright)%2B3O_2%5Cleft(g%5Cright)) c)
c)
%2BO_2%5Cleft(g%5Cright)-%3E2NO_2%5Cleft(g%5Cright))
%2BFe_2O_3%5Cleft(s%5Cright)-%3EAl_2O_3%5Cleft(s%5Cright)%2B2Fe%5Cleft(s%5Cright))
g)
%2B2KOH%5Cleft(aq%5Cright)-%3EK_2SO_4%5Cleft(aq%5Cright)%2B2H_2O%5Cleft(l%5Cright))
%2B25O_2%5Cleft(g%5Cright)-%3E16CO_2%5Cleft(g%5Cright)%2B18H_2O%5Cleft(g%5Cright))
%2B3O_2%5Cleft(g%5Cright)-%3E2Fe_2O_3%5Cleft(s%5Cright)) b)
b)
%2B3H_2%5Cleft(g%5Cright)-%3E2NH_3%5Cleft(g%5Cright))
c)
%2B6O_2%5Cleft(g%5Cright)-%3E6CO_2%5Cleft(g%5Cright)%2B6H_2O%5Cleft(l%5Cright))
%2BO_2%5Cleft(g%5Cright)-%3E2H_2O%5Cleft(l%5Cright))
%2BPb%5Cleft(s%5Cright)-%3E2Ag%5Cleft(s%5Cright)%2BPb%5Cleft(NO_3%5Cright)_2%5Cleft(aq%5Cright))
%2B2H_2O%5Cleft(l%5Cright)-%3E2NaOH%5Cleft(aq%5Cright)%2BH_2%5Cleft(g%5Cright))
-%3EK_2O%5Cleft(g%5Cright)%2BH_2O%5Cleft(g%5Cright)%2B2CO_2%5Cleft(g%5Cright))
_2%5Cleft(aq%5Cright)%2B2HNO_3%5Cleft(l%5Cright)-%3ECa(NO_3)_2%5Cleft(l%5Cright)%2B2H_2O%5Cleft(l%5Cright)) d)
d)
%2BO_2%5Cleft(g%5Cright)-%3E2CuO%5Cleft(s%5Cright))
%2BHCl%5Cleft(aq%5Cright)-%3ENaCl%5Cleft(aq%5Cright)%2BCO_2%5Cleft(g%5Cright)%2BH_2O%5Cleft(l%5Cright))
a) (s)
b) (s)
c) (g)
d) (s)
e) (l)
f) (g)
g) (aq)
h) (l)
1.9
a)
b)
e)
%2B6H_2O%5Cleft(l%5Cright)-%3EC_6H_%7B12%7DO_6%5Cleft(s%5Cright)%2B6O_2%5Cleft(g%5Cright))
f)
f)
g)
h)
1.10
a)
c)
d)
e)
1.11
a)
b)
c)
e)
%2BCO_2%5Cleft(g%5Cright)-%3ECuCO_3%5Cleft(s%5Cright))
f)
Kpl.1.1
1.2
a) -
b) +
c) -
d) +
e) -
f) -
1.3
 Entropia kasvaa
Entropia kasvaa
 Entalpia
Entalpia
 Eksoterminen reaktio
Eksoterminen reaktio
 Entropia
Entropia
 Spontaani reaktio
Spontaani reaktio
 Entropiamuutos
Entropiamuutos
 Entalpiamuutos
Entalpiamuutos
 Gibbsin energiamuutos
Gibbsin energiamuutos
 Aktivoitumisenergia
Aktivoitumisenergia



1.5
1.6
a) -
b) +
c) -
d) +
e) -
f) -
1.3
1.5
1.6
Kertaa osaamasi
t.1
a) 2
b) 3
c) 2
d) 3
e) 4
t.2
a) Väärin, 0,022g
b) Oikein
c) Oikein
d) Väärin, 0,045kg
e) Oikein
f) Väärin, 0,0163dm³
t.3
a)
b)
c)
t.4
a)
b)
t.5
a)
ratkaistaan liuokseen valmistamiseen tarvitun ainemäärä kaavalla
b)
- Punnitaan 4,00 grammaa natriumhydroksidia mahdollisimman tarkasti.
- Liuotetaan natriumhydroksidi dekantterilasissa lopputilavuutta pienempään tilavuuteen tislattua vettä.
- Kun natriumhydroksidi on täysin liuennut, siirretään liuos 200 ml:n mittapulloon.
- Huuhdotaan dekantterilasi muutaman kerran pienellä määrällä vettä.
- Täytetään mittapullo merkkiviivan saakka ja sekoitetaan liuosta muutaman kerran,
- Tehdään mittapulloon tarvittavat merkinnät ja lisätään syövyttävän aineen varoitusmerkki.
c)
Koska natriumhydroksidi on syövyttävää ainetta, tulee sitä punnittaessa ja liuotettaessa käyttää suojalaseja ja suojakäsineitä. Liuoksen säilytyspulloon laitetaan varoitusmerkki syövyttävästä aineesta.
t.6
a)
Ympäristölle haitallinen
b)
vesiliuos
c)
Täyspipetillä, sillä voidaan saada tarkin tilavuuden mittaus
d)
100 millilitran mittapulloon
e)




%3Dc_1%5Cleft(CuSO_4%5Cright)%5Ccdot%20V_1%3D0%7B%2C%7D0100%5C%20%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%5Ccdot0%7B%2C%7D00500dm%5E3%3D5%7B%2C%7D0000%5Ccdot10%5E%7B-5%7Dmol) Ratkaistaan laimennoksen kuparisulfaattikonsentraatio suureyhtälöstä
Ratkaistaan laimennoksen kuparisulfaattikonsentraatio suureyhtälöstä

%7D%7BV_2%7D%3D%5Cfrac%7B5%7B%2C%7D0000%5Ccdot10%5E%7B-5%7Dmol%7D%7B0%7B%2C%7D100dm%5E3%7D%3D5%7B%2C%7D0000%5Ccdot10%5E%7B-4%7D%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%5Capprox0%7B%2C%7D500%5C%20%5Cfrac%7Bmmol%7D%7Bdm%5E3%7D)
f)
%5Cright)%3D0%7B%2C%7D0100%5Cfrac%7Bmol%7D%7Bdm%5E3%7D)
%3D50%7B%2C%7D0ml%3D0%7B%2C%7D500dm%5E3)
%3D249%7B%2C%7D700%5Cfrac%7Bg%7D%7Bmol%7D)

%3Dc%5Cleft(CuSO_4%5Ccdot5H_2O%5Cright)%5Ccdot%20V%5Cleft(liuos%5Cright)%3D0%7B%2C%7D100%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%5Ccdot0%7B%2C%7D0500dm%5E3%3D5%7B%2C%7D0000%5Ccdot10%5E%7B-4%5C%20%7Dmol)
Lasketaan kidevedellisen kuparisulfaatin massa:
%3Dn%5Cleft(CuSO_4%5Ccdot5H_2O%5Cright)%5Ccdot%20M%5Cleft(CuSO_4%5Ccdot5H_2O%5Cright)%3D5%7B%2C%7D0000%5Ccdot10%5E%7B-4%7Dmol%5Ccdot249%7B%2C%7D700%5Cfrac%7Bg%7D%7Bmol%7D%3D0%7B%2C%7D12485g%5Capprox0%7B%2C%7D125g)
t.7
%3D69%5C%25%3D0%7B%2C%7D69)
%3D1%7B%2C%7D41%5Cfrac%7Bg%7D%7Bcm%5E3%7D)
%3D63%7B%2C%7D018%5Cfrac%7Bg%7D%7Bmol%7D)
%3D%5Cfrac%7Bm%5Cleft(HNO_3%5Cright)%7D%7BM%5Cleft(HNO_3%5Cright)%7D%3D%5Cfrac%7B927%7B%2C%7D9g%7D%7B63%7B%2C%7D018%5Cfrac%7Bg%7D%7Bmol%7D%7D%3D15%7B%2C%7D44mol)
%3D%5Cfrac%7Bn%5Cleft(HNO_3%5Cright)%7D%7BV%5Cleft(HNO_3%5Cright)%7D%3D%5Cfrac%7B15%7B%2C%7D44mol%7D%7B1%7B%2C%7D0dm%5E3%7D%3D15%7B%2C%7D44%5Cfrac%7Bmol%7D%7Bdm%5E3%7D%5Capprox15%5Cfrac%7Bmol%7D%7Bdm%5E3%7D)
t.8
 Ioniyhdiste
Ioniyhdiste
_3) Ioniyhdiste
Ioniyhdiste
 Molekyyliyhdiste
Molekyyliyhdiste
_2) Ioniyhdiste
Ioniyhdiste
 Molekyyliyhdiste
Molekyyliyhdiste
_2) Ioniyhdiste
Ioniyhdiste
 Molekyyliyhdiste
Molekyyliyhdiste
_2) Molekyyliyhdiste
Molekyyliyhdiste
t.6
a)
Ympäristölle haitallinen
b)
vesiliuos
c)
Täyspipetillä, sillä voidaan saada tarkin tilavuuden mittaus
d)
100 millilitran mittapulloon
e)
Ratkaistaan laimennokseen tulevan kuparisulfaatin ainemäärä suureyhtälöstä:
f)
Ratkaistaan, mikä ainemäärä kidevedellistä kuparisulfaattia oli valmistetussa liuoksessa
Lasketaan kidevedellisen kuparisulfaatin massa:
t.7
Voidaan oleta annetun tiehyden nojalla että yhden liuoslitran (dm³) massa on siis 
Massaprosenttisen osuuden perusteella typpihapon osuus yhden liuoslitran massasta on %3D0%7B%2C%7D69%5Ccdot1410g%3D927%7B%2C%7D9g)
Yhdessä liuoslitrassa olevan typpihapon ainemäärä on
typpihapon konsentraatioksi saadan
t.8